Regularization(정직화)
오버피팅(train set은 매우 잘 맞히지만, validation, test set은 맞히지 못하는 현상)을 해결하기 위한 방법 중 하나
- L1 Regularization
- L2 Regularization
- Dropout
- Batch Normalization
L1 Regularization(Lasso)
\[\hat{\beta}^{lasso} := argmin_\beta \frac{1}{2N} \sum_{i=1}^{N} (y_i - \beta_0 - \sum_{j=1}^{p}x_{ij}\beta_j)^2 + \lambda \sum_{j=1}^{p}|\beta_j|\]
뒤쪽 항이 없다면 Linear Regression과 같은 식이 된다.
Lp Norm
\[\left\| x\right\|_p := (\sum_{i=1}^{n}|x_i|^p)^{1/p}\]
p=1인 경우 L1 Norm 은 아래와 같이 된다.
\[\left\| x\right\|_1= \sum_{i=1}^{n}|x_i|\]
p값이 1이기 때문에 L1 Regularization이라고 부른다.
\[\hat{\beta}^{lasso} := argmin_\beta \frac{1}{2N} \sum_{i=1}^{N} (y_i - \beta_0 - \sum_{j=1}^{p}x_{ij}\beta_j)^2 + \lambda \sum_{j=1}^{p}|\beta_j|\]
L1 Regularization의 정의는 위와 같은데, X와Y 변수를 N, p=1로 하는 선형회귀 식은 아래와 같이 된다.
\[\hat{\beta}^{lasso} = argmin_\beta \frac{1}{2N} \sum_{i=1}^{N} (y_i - \beta_0 - x_i\beta_1)^2 + \lambda|\beta_1|\]
B1, B0의 미분값이 0이 되는 지점을 통해 최적의 값을 구해보면 아래의 값만 남게된다.
\[0 = \frac{1}{N} \sum_{i=1}^{N} x_i(y_i - \beta_0 - x_i\beta_1) + \lambda\]
\[0 = \frac{1}{N} \sum_{i=1}^{N}(y_i - \beta_0 - x_i\beta_1)\]
위 두 식을 정리하면 아래와 같다.
\[\beta_1 = \frac{-\beta_0 \bar{x}+ \bar{xy} + \lambda}{x^2}\]
\[\beta_0 = \bar{y} - \bar{x}\beta_1\]
p=1인 경우 B0에 대해 미분하는 과정에서 lambda값이 사라지므로 Regularization 효과를 볼 수 없다. 이는 X가 1차원인 선형회귀분석에서는 L1 Regularization이 의미가 없다는 것을 의미한다.
그러므로, L1 Regularization을 사용할 때는 X가 2차원 이상인 여러 컬럼 값이 있는 데이터일 때 실제 효과를 볼 수 있다.
L2 Regularization(Ridge)
\[\hat{\beta}^{Ridge} := argmin_\beta \frac{1}{2N} \sum_{i=1}^{N} (y_i - \beta_0 - \sum_{j=1}^{p}x_{ij}\beta_j)^2 + \lambda \sum_{j=1}^{p}\beta_j^2\]
수식의 뒷부분이 L2 Norm값과 같다.
L1 L2의 차이점
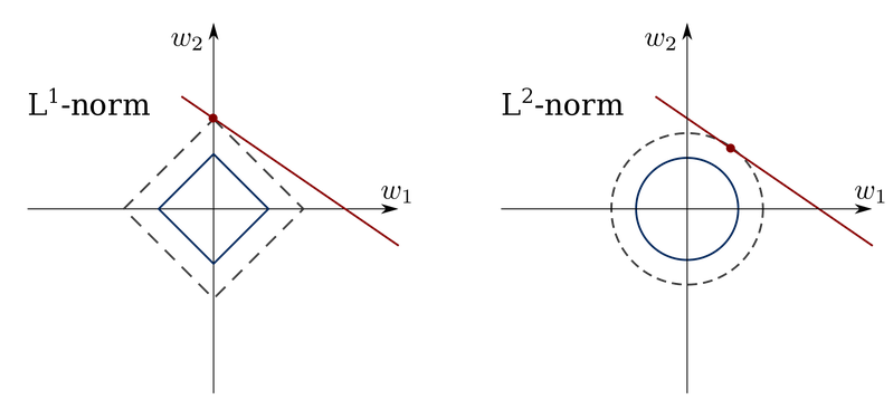
L1 Regularizaion(Lasso)는 를 이용하여 마름모 형태의 제약조건이 생깁니다. 그리고 위의 등고선처럼 보이는 내용은 우리가 풀어야 하는 문제입니다. 이 문제가 제약조건과 만나는 지점이 해가 됩니다. 그래서 L1 Regularization에서는 몇 개의 축에서 값을 0으로 보냅니다.
이와 다르게 L2 regularization은 이므로 원의 형태로 나타나게 됩니다. 그러므로 0에 가지는 않고 0에 가깝게 감을 확인할 수 있습니다. 또한 제곱이 들어가 있기 때문에 절댓값으로 L1 Norm을 쓰는 Lasso보다는 수렴이 빠르다는 장점이 있습니다.
Normalization(정규화)
데이터의 형태를 좀 더 의미 있게, 혹은 학습에 적합하게 전처리 하는 과정
데이터를 z-score로 바꾸거나 minmax scaler를 사용하여 0과 1 사이의 값으로 분포를 조정
- 금액과 같은 큰 범위의 값(10,000 ~ 10,000,000)과 시간(0~24) 의 값이 들어가는 경우, 학습 초반에는 데이터 거리 간의 측정이 피처 값의 범위 분포 특성에 의해 왜곡되어 학습에 방해를 받게 되는 문제가 있다.
- Normalization은 이를 모든 피처의 범위 분포를 동일하게 하여 모델이 풀어야 하는 문제를 좀 더 간단하게 바꾸어 주는 전처리 과정
'Aiffel > Fundamental' 카테고리의 다른 글
| TensorFlow2 API (0) | 2022.01.28 |
|---|---|
| seq2seq(Sequence to Sequence) (0) | 2022.01.27 |
| 텍스트 요약(Text Summarization) (0) | 2022.01.27 |
| Softmax 함수와 Cross Entropy (0) | 2022.01.24 |
| 로지스틱 회귀분석(Logistic Regression) (0) | 2022.01.24 |


댓글