본 글은 Havard University Statistics 110 강의를 듣고 정리한 내용입니다.
Poisson Distribution
X ~ Pois(λ)
포아송 분포는 많은 시도의 횟수를 시행하고, 성공 확룰이 매우 작은 경우에 성공의 수를 count 할 때 많이 사용한다.
Poisson Paradign (Pois Approximation, 포아송 근사)
event Aj, P(Aj) = pj 에서 n은 매우 큰 수이고 pj는 매우 작은 수라고 할 때,
event 끼리 독립이면(혹은 약한 종속성을 가지고 있는 경우) event Aj는 포아송 분포로 근사할 수 있다.
Ex. Raindrops, Birthday Problem
PDF(Probability Density Function, 확률밀도함수)
PDF of 확률변수 X
원칙적으로 P(X=x) = 0이나 density 의 개념을 이용하여 아래와 같이 구할 수 있다.
확률변수 X가 PDF f를 가지고 있을 때, 확률변수 X의 CDF는 아래와 같다.
확률변수 X가 CDF F를 가지고 있을 때, 확률변수 X의 PDF는 미적분학의 기본 정리에 의해 아래와 같이 나타난다.

Uniform(균등분포)
X ~ Unif(a, b), 특정 범위가 뽑힐 확률이 그 범위의 크기에 비례하는 분포
f(x) = c if a ≤ x ≤ b, 0 otherwise
E(X) = (a + b) / 2
균등분포의 일반성
균등분포의 대칭성
균등분포의 선형변환
정규분포
중심극한정리 : 여러개의 독립적이고 동일한 확률변수를 더했을 때, 그 합의 분포가 정규분포를 따라 갈 것이다.


표준정규분포의 CDF
E(Z) = 0 (정규분포의 대칭성)
Var(Z) = E(Z^2)
E(Z^3) = 0 (LOTUS)
일반정규분포
평균과 분산
X, Y가 독립일 경우는 위 식 성립
68-95-99.7% Rule
- P(|X-μ| ≤ σ) ≒ 0.68
- P(|X-μ| ≤ 2σ) ≒ 0.95
- P(|X-μ| ≤ 3σ) ≒ 0.997
Poisson Distribution
Binomial Distribution
이산확률변수에서의 LOTUS(무의식적인 통계학자 법칙) 증명
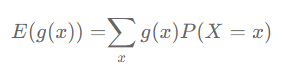
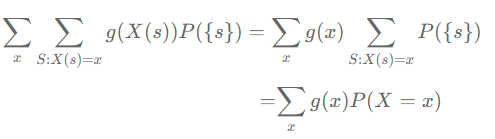
'Study > 통계학' 카테고리의 다른 글
| 22. 변수변환과 합성곱(Transformations and Convolutions) (0) | 2022.02.21 |
|---|---|
| 21. 공분산과 상관계수(Covariance and Correlation) (0) | 2022.02.20 |
| 4~10강 Review (0) | 2022.02.13 |
| 20. 다항분포 및 코시분포(Multinomial and Cauchy) (0) | 2022.02.07 |
| 19. 결합, 조건부, 주변 확률질량함수(Joint, Conditional, and Marginal Distributions) (0) | 2022.02.06 |

댓글