본 글은 Havard University Statistics 110 강의를 듣고 정리한 내용입니다.
무기억성(Memoryless property)
T = 기대수명
E(T|T>20) > E(T)
만약 무기억성이라면, E(T|T>20) = 20 + E(T)
if X is positive continuous r.v. with memoryless property, then X ~ Expo(λ) for some λ (지수분포의 특성)
Proof
Let F be the CDF of X, G(x) = P(X>x) = 1-F(x)
Memoryless Property G(s+t) = G(s)G(t)
if s = t -> G(2t) = G(t)^2, G(3t) = G(2t)G(t) = G(t)^3, G(kt) = G(t)^k (k는 양의 정수)G(t/2) = G(t)^(1/2), G(t/3) = G(t)^(1/3), G(t/k) = G(t)^(1/k), G(mt/n) = G(t)^(m/n)∴ G(xt) = G(t)^x for all real x > 0
t = 1 -> G(x) = G(1)^x = e^(xlnG(1)) = e^-λx (lnG(1) = λ)
Moment Generating Function(적률생성함수)
Defn. A r.v. X has MGF M(t) = E(e^tX)
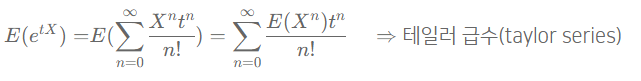
- n차적률 E(X^n)은 M에서 테일러 급수에서 t^n/n!의 계수이다. (i.e. M^(n)(0) = E(X^n))
- 같은 MGF를 가진 서로 다른 두 확률변수는 같은 확률분포를 가진다.(같은 CDF를 가짐)
- 확률변수 X는 MGF M_X, Y는 MGF M_Y를 가질 때, X+Y의 기댓값 E(e^{t(X+Y)}) = E(e^{tX})E(e^{tY})= M_X(t) * M_Y(t)를 만족한다. (X,Y는 독립)
확률분포의 MGF
X ~ Bern(p), MGF M(t) = E(e^tX) = pe^t + q
X ~ Bin(n,p) -> M(t) = (pe^t + q)^n


라플라스의 후속규칙(Laplace's Rule of Succession)
내일 해가 뜰 확률은 얼마인가?
p가 주어졌을 때, X1, X2, .... i.i.d. Bern(p), 그러나 알지 못하는 p를 어떻게 구하는가?
- 베이지안 : p를 확률변수로 봄
Let p ~ Unif(0, 1), 사전확률
Let Sn = X1 + ... + Xn
Sn | p ~ bin(n, p), p ~ Unif(0, 1)
- 독립적이며 같은 분포를 따르는 베르누이 p의 합은 이항분포이다.
사후확률 p | Sn(Xn들 중에 얼마나 1을 가지는가) , P(Xn+1 = 1 | Sn = n) (지난 n일동안 해가 떴을 때, 내일 해가 뜰 확률)

- P(Sn=k) = ∫[p=0~1] P(Sn=k|p) f(p)dp (전확률의 법칙 continuous 버전)
f(p|Sn=n)의 경우 함수는 p^n에 비례하고, ∫[0~1]cP^n = 1이 되어야 하기 때문에, 결과적으로 (n+1)p^n이 된다.
'Study > 통계학' 카테고리의 다른 글
| 19. 결합, 조건부, 주변 확률질량함수(Joint, Conditional, and Marginal Distributions) (0) | 2022.02.06 |
|---|---|
| 18. 적률생성함수_2 (MGFs Continued) (0) | 2022.02.05 |
| 16. 지수분포(Exponential Distribution) (0) | 2022.02.01 |
| 15. Midterm Review (0) | 2022.01.31 |
| 14. 위치, 척도 및 무의식적인 통계학자의 법칙(Location, Scale, and LOTUS) (0) | 2022.01.29 |




댓글