본 글은 주재걸교수님의 인공지능을 위한 선형대수 강의를 듣고 정리한 내용입니다.
머신러닝에서 Eigendecomposition
- often handle symmetric positive definite matrix
- A : 3명에 대한 10개의 feature를 가지는 matrix
- ATA : inner product 기준으로 두 사람에 대한 similarity
- pariwise inner product similarity
- AAT : 특정 feature에 대한 inner product 를 기준으로 한 similarity
- principal component analysis
- gram matrix(feature inner product similarity) in style transfer
Low Rank Approximation of a Matrix
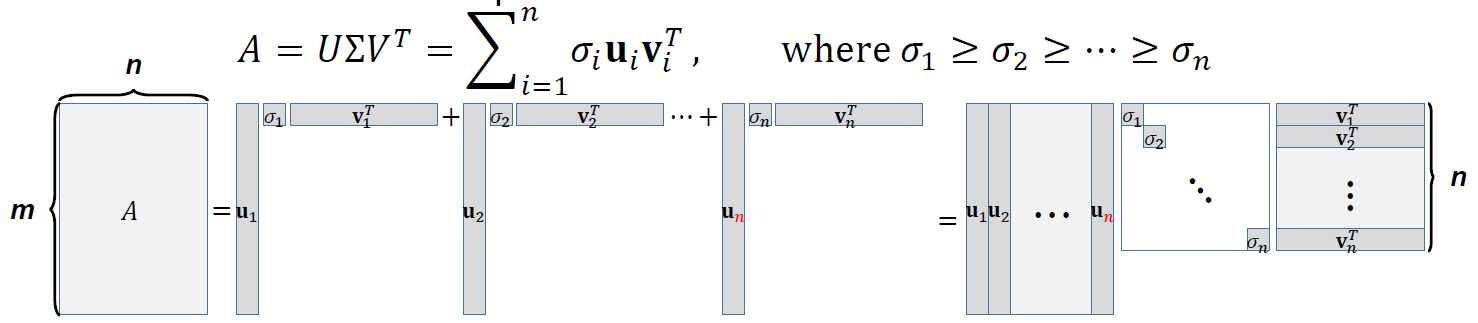
Rank : 여러 컬럼들을 만들기 위해 필요한 column space의 basis 갯수
- Consider the problem of the best low rank approximation of 𝐴:
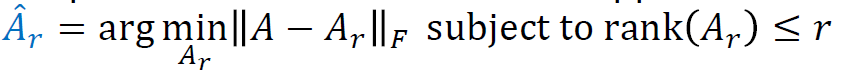
- Optimal Solution
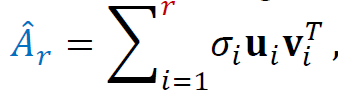
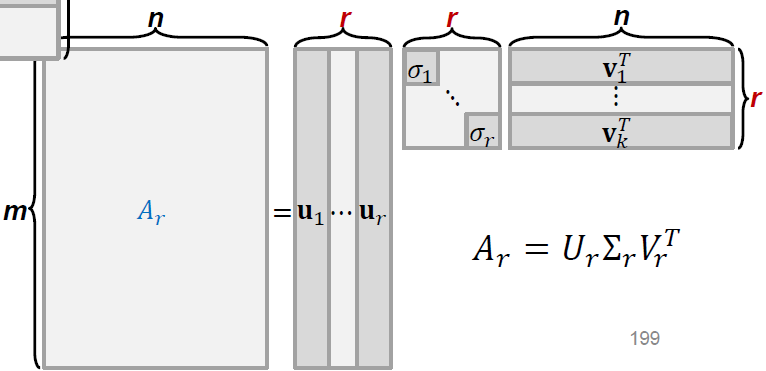
Dimension Reducing Transformation
- 선형 변환을 통한 차원 축소
- Can we find the linear transformation, 𝐲𝑖=𝐺^𝑇𝐱𝑖, where the columns of 𝐺∈ℝ𝑚×𝑟 are orthonormal
- Y = G^TX, pairwise similarity
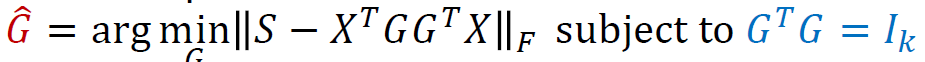
'Study > 선형대수학' 카테고리의 다른 글
| 5-1 특이값 분해 (0) | 2022.01.07 |
|---|---|
| 4-5. 고유값 분해와 선형변환 (1) | 2022.01.06 |
| 4-4. 대각화 (0) | 2022.01.05 |
| 4-3. 특성방정식 (0) | 2022.01.05 |
| 4-2. 영공간과 직교여공간 (0) | 2022.01.05 |




댓글