Competition : https://www.kaggle.com/c/house-prices-advanced-regression-techniques/overview
Code : https://www.kaggle.com/pmarcelino/comprehensive-data-exploration-with-python
Description

Dataset
- train.csv - the training set
- test.csv - the test set
- data_description.txt - 각 컬럼에 대한 자세한 설명
- sample_submission.csv - a benchmark submission from a linear regression on year and month of sale, lot square footage, and number of bedrooms
Data column에 대한 설명은 컬럼이 너무 많아 생략
1. Understand data

- Type : 변수들의 데이터 타입은 numerical과 categorical이 있음.
- Segment : 변수들을 segment 했을 때, building, space, location 3개로 정의할 수 있다.
- building : 건물의 물리적 특성과 관련된 변수(e.g. OverallQual : Overall material and finish quality)
- space : 집의 공간 속성을 보고하는 변수(e.g. TotalBsmtSF : Total square feet of basement area)
- location : 집이 위치한 장소에 대한 정보(e.g. Neighborhood : Physical locations within Ames city limits)
- Expectation : 변수들이 SalePrice에 영향을 주는 것에 대한 기대, categorical scale를 사용할 수 있다. (High, medium, Low)
- Conclusion : 데이터를 간략히 살펴본 후의 데이터의 중요성에 대한 결론.

데이터를 분석하기 전에 위의 과정들을 거치고, Expectation에 대한 몇가지 질문을 던진다.
- 우리가 이러한 변수들을 실제 집을 구매할 때 고려하는가?
- 고려한다면, 얼마나 중요한가?
- 이러한 정보들이 다른 변수들에 설명되어있는가?
위 질문을 통해 기대치를 설정할 수 있고, 이를 SalePrice와의 scatterplot을 그려 Conclusion에 대한 답을 할 수 있다. 이 과정을 통해 이 문제에서 중요한 역할을 하는 변수를 찾을 수 있다.
- OverallQual (which is a variable that I don't like because I don't know how it was computed; a funny exercise would be to predict 'OverallQual' using all the other variables available).
- YearBuilt.
- TotalBsmtSF.
- GrLivArea.
2. Analysing Target variable


- Deviate from the normal distribution.
- Have appreciable positive skewness.
- Skewness: 1.882876
- Kurtosis: 6.536282
- Show peakedness.
Skewness(왜도) : 분포의 비대칭성을 나타내는 척도
- Positive Skewness : 데이터의 중심(평균)이 정규분포보다 왼쪽으로 치우쳐져 있음.(분포의 peakedness가 왼쪽)
- 꼬리는 오른쪽으로 길어짐, Right-skewed라고도 표현
- Negative Skewness : 데이터의 중심(평균)이 정규분포보다 오른쪽으로 치우쳐져 있음.(분포의 peakedness가 오른쪽)
- 꼬리는 왼쪽으로 길어짐. Left-skewed라고도 표현
- 왜도값이 -2 ~ 2 정도는 크지 않다고 판단. 절대값 3 미만이면 기준에 부합
kurtosis(첨도) : 측정치의 빈도수를 그래프로 표현했을 때 나타나는 분포의 뾰족한 정도
- 분포의 정점(peakedness)를 뜻하는 그리스어에서 파생
- 샘플의 점수가 평균을 중심으로 가까이 몰려있을수록 첨도가 커짐
- 뾰족한 모양의 성질에 따라 중첨(mesokurtic, 정규분포 모양), 고첨(leptokurtic, 정규분포보다 더 뾰족), 저첨(playkurtic, 정규분포보다 더 완만)으로 분류
- 정규분포의 첨도는 0이며, 첨도가 0보다 크면 고첨, 0보다 작으면 저첨
- 첨도가 크면 이상치가 많아짐, 절대값 7 미만이면 기준에 부합
Important variables와 SalePrice EDA


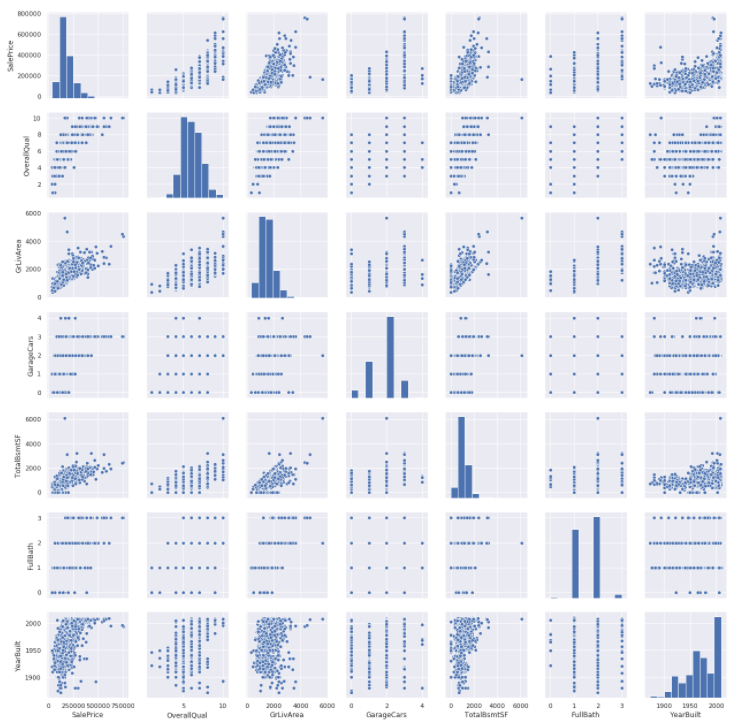
SalePrice와 GrLivArea, TotalBsmtSF 간에는 Linear Relationship이 보인다.

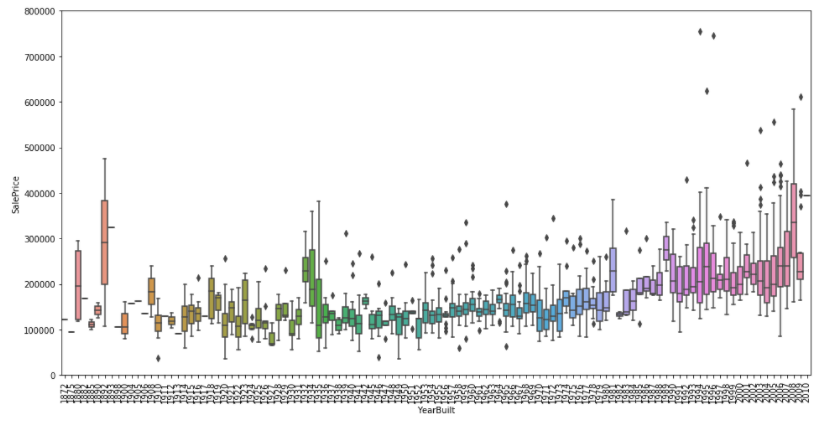
OverallQual은 category가 커질수록 값이 커지는 경향을 보이나, YearBuilt는 큰 상관관계는 보이지 않는다.
3. Correlation
corrmat = df_train.corr()
f, ax = plt.subplots(figsize=(12, 9))
sns.heatmap(corrmat, vmax=.8, square=True);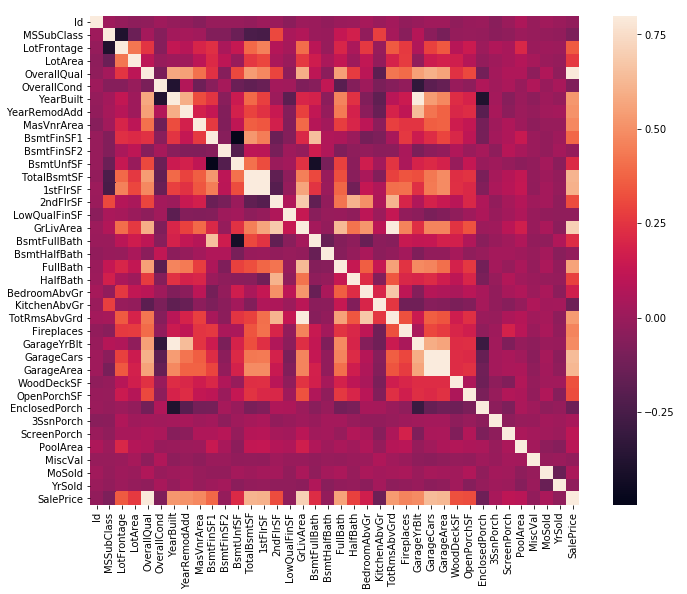
몇가지 상관관계가 높은 변수들이 보이나, 한눈에 보기 어려움
SalePrice와 correlation이 높은 10개의 변수 추출
#saleprice correlation matrix
k = 10 #number of variables for heatmap
cols = corrmat.nlargest(k, 'SalePrice')['SalePrice'].index
cm = np.corrcoef(df_train[cols].values.T)
sns.set(font_scale=1.25)
hm = sns.heatmap(cm, cbar=True, annot=True, square=True, fmt='.2f', annot_kws={'size': 10}, yticklabels=cols.values, xticklabels=cols.values)
plt.show()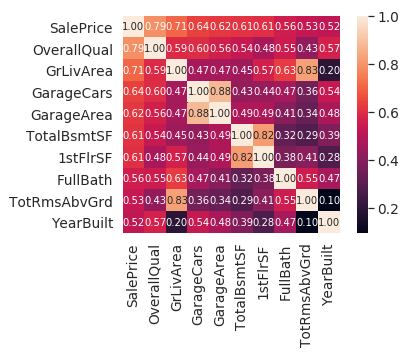
- 위에서 Expectation이 높다고 예상한 OverallQual, GrLivArea, TotalBsmtSF의 상관관계가 높게 나왔음.
- 'GarageCars' 와 'GarageArea' 는 둘다 높은 상관관계를 보이나, 이 두 변수는 서로 영향을 주는 인자이기 때문에 성관계수가 더 높은 GarageCars만을 남긴다.
- 'TotalBsmtSF' and '1stFlrSF' , 'TotRmsAbvGrd' and 'GrLivArea' 또한 위 이유와 마찬가지
- TotalBsmtSF: Total square feet of basement area
- 1stFlrSF: First Floor square feet
- TotRmsAbvGrd: Total rooms above grade (does not include bathrooms)
- GrLivArea: Above grade (ground) living area square feet
4. Missing data
total = df_train.isnull().sum().sort_values(ascending=False)
percent = (df_train.isnull().sum()/df_train.isnull().count()).sort_values(ascending=False)
missing_data = pd.concat([total, percent], axis=1, keys=['Total', 'Percent'])
missing_data.head(20)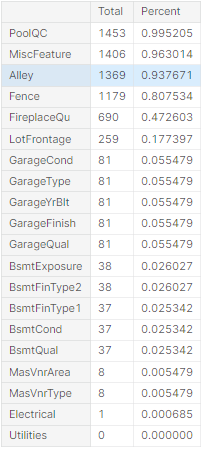
- 데이터의 15% 이상 결측치가 있는 경우 변수 제거
- GarageX, BsmtX의 경우 결측치의 갯수가 같은 경우가 많고, 위 변수들보다 같은 내용을 더 잘 표현하고 결측치가 없는 변수가 따로 존재하기 때문에, 이 변수들은 모두 제거해준다.
- GarageX -> GarageCar, BsmtX -> TotalBsmtSF
- 상태에 대한 정보를 numerical 정보가 담겨있는 변수로 판단??
- Masonry veneer(석조 베니어판) 관련 정보는 YearBuilt , OverallQual 와 연관성이 많음.
- MasVnrArea: Masonry veneer area in square feet
- MasVnrType: Masonry veneer type
- Electrical은 1개의 관측치에만 결측치가 존재하기 때문에 해당 관측치 제거
df_train = df_train.drop((missing_data[missing_data['Total'] > 1]).index,1)
df_train = df_train.drop(df_train.loc[df_train['Electrical'].isnull()].index)
df_train.isnull().sum().max()
>>>
05. Outlier
Outliers can markedly affect our models and can be a valuable source of information, providing us insights about specific behaviours.
outlier를 정의하기 위한 threshold값을 결정하기 위해, 우선 데이터를 standardization해준다.
saleprice_scaled = StandardScaler().fit_transform(df_train['SalePrice'][:,np.newaxis]);
low_range = saleprice_scaled[saleprice_scaled[:,0].argsort()][:10]
high_range= saleprice_scaled[saleprice_scaled[:,0].argsort()][-10:]
print('outer range (low) of the distribution:')
print(low_range)
print('\nouter range (high) of the distribution:')
print(high_range)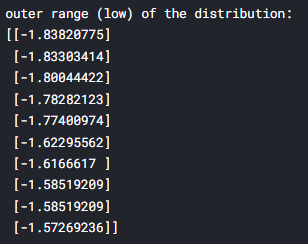
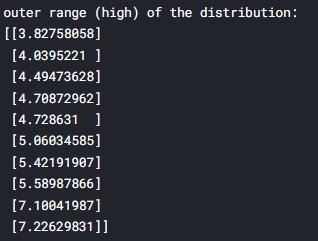
낮은 값들은 0과 가까운 값을 가지나, 높은 값들은 7이 넘는 값을 가진다. 여기선 이를 제거하지는 않지만 주의깊게 볼 필요는 있다.
Bivariate analysis
var = 'GrLivArea'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000));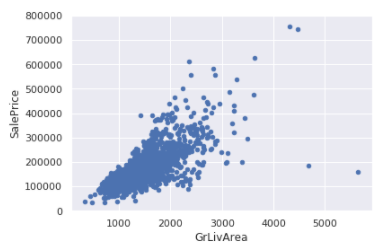
SalePrice의 경우 7이 넘는 값들이 어느정도의 경향성을 따라가는 것을 확인할 수 있다. 그러나 GrLivArea가 가장 큰 2개의 값은 경향에서 많이 벗어나있다. 여기서는 이를 제거해준다.
6. Getting hard core
'SalePrice'가 다변량 기술을 적용할 수 있도록 하는 통계적 가정
Now it's time to go deep and understand how 'SalePrice' complies with the statistical assumptions that enables us to apply multivariate techniques
- Normality(정규성)
- 데이터가 정규분포를 만족하는지를 나타내는 가정
- 정규성을 만족하지 않는 변수를 distplot, probplot을 통해 확인
- Histogram - Kurtosis and skewness.
- Normal probability plot - Data distribution should closely follow the diagonal that represents the normal distribution.
- 만족하지 않는 경우는 log scale 변환 진행
sns.distplot(df_train['SalePrice'], fit=norm);
fig = plt.figure()
res = stats.probplot(df_train['SalePrice'], plot=plt)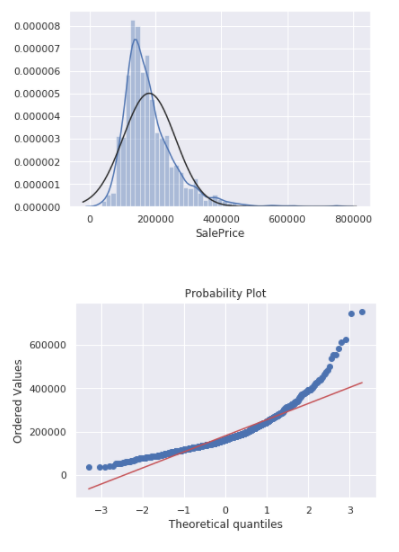
peakedness를 보이고, positive skewness에 diagonal line을 따르지 않기 때문에 SalePrice는 normal하지 않다.
df_train['SalePrice'] = np.log(df_train['SalePrice'])
sns.distplot(df_train['SalePrice'], fit=norm);
fig = plt.figure()
res = stats.probplot(df_train['SalePrice'], plot=plt)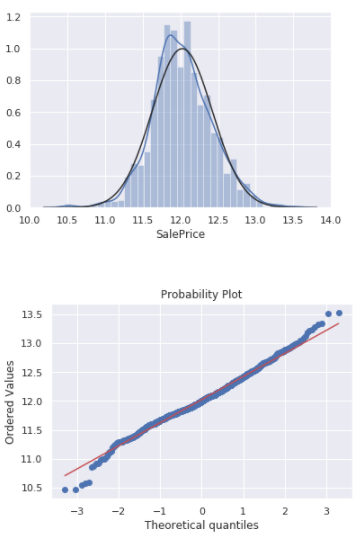
GrLivArea, TotalBsmtSF에 대해서도 같은 방식으로 진행
0의 값이 많이 존재하는 경우는 log변환을 할 수 없기 때문에, 0이 아닌 경우에 대해서만 log변환을 진행한 후, 그 데이터에 대해 정규성을 확인한다.
- Homoscedasticity(등분산성)
- 종속 변수가 독립 변수의 범위 내에서 동일한 수준의 분산을 나타낸다는 가정
- scatterplot을 통해 등분산성 확인하는 것이 가장 좋은 접근 방법이다.
plt.scatter(df_train['GrLivArea'], df_train['SalePrice']);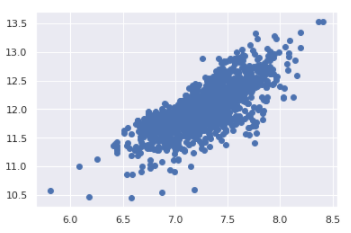
- Linearity(선형성)
- 데이터의 분포가 선형 패턴을 띄는지에 대한 가정
- Absence of correlated errors(잔차의 상관성)
- 하나의 오류가 다른 오류와 상관관계를 가지는 경우 발생
참고 자료
'Kaggle' 카테고리의 다른 글
| New York City Taxi Trip Duration 코드리뷰 (0) | 2022.02.01 |
|---|---|
| House Prices - Advanced Regression Techniques 코드리뷰 2 (0) | 2022.01.26 |
| Bike Sharing Demand 코드리뷰 (0) | 2022.01.25 |



댓글