본 글은 주재걸교수님의 인공지능을 위한 선형대수 강의를 듣고 정리한 내용입니다.
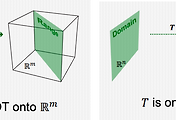
The most important aspect of the least-squares problem is that no matter what x we select, the vector 𝐴𝐱 will necessarily be in the column space Col 𝐴
Thus, we seek for x that makes 𝐴𝐱 as the closest point in Col 𝐴 to 𝐛.

𝐛 − 𝐴𝐱 ⊥ (𝑥1a1 + 𝑥2a2 ⋯ + 𝑥𝑝a𝑛) for any vector x

given a least squares problem, 𝐴𝐱 ≃ 𝐛, we obtain

which is called a normal equation
'Study > 선형대수학' 카테고리의 다른 글
| 3-4. Orthogonal Projection (0) | 2022.01.04 |
|---|---|
| 3-3. 정규방정식 (0) | 2022.01.03 |
| 3-1. Least Squares Problem (0) | 2022.01.01 |
| 2-6. 전사함수와 일대일함수 (0) | 2021.12.30 |
| 2.5 선형변환 (0) | 2021.12.29 |
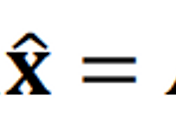
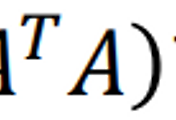
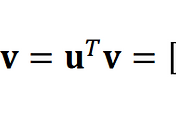
댓글