본 글은 주재걸교수님의 인공지능을 위한 선형대수 강의를 듣고 정리한 내용입니다.
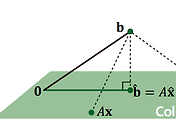
the case of invertible 𝐶 = 𝐴^𝑇𝐴, consider the orthogonal projection of 𝐛 onto Col 𝐴 as

Orthogonal and Orthonormal Sets
orthogonal set if each pair of distinct vectors from the set is orthogonal That is, if 𝐮𝑖 ⋅ 𝐮𝑗 = 0 whenever 𝑖 ≠ 𝑗.
orthonormal set if it is an orthogonal set of unit vectors.
Orthogonal and Orthonormal Basis
subspace에 대한 basis 중 Orthogonal을 만족하는 Basis
Gram–Schmidt process
Orthogonal Projection 𝐲 ො of 𝐲 onto Line


Orthogonal Projection 𝐲 ො of 𝐲 onto Plane

각 span에 대해 projection 한 후 더해주는 것과 같은 결과를 가진다.

Transformation: Orthogonal Projection
Consider a transformation of orthogonal projection 𝐛 መ of 𝐛, given orthonormal basis 𝐮1, 𝐮2 of a subspace W

'Study > 선형대수학' 카테고리의 다른 글
| 4-1. 고유벡터와 고유값 (0) | 2022.01.05 |
|---|---|
| 3-5. 그람-슈미트 직교화와 QR 분해 (0) | 2022.01.04 |
| 3-3. 정규방정식 (0) | 2022.01.03 |
| 3-2 Least Squares와 그 기하학적 의미 (0) | 2022.01.03 |
| 3-1. Least Squares Problem (0) | 2022.01.01 |

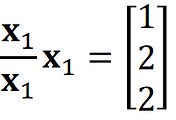
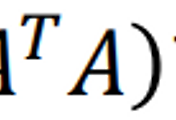
댓글