본 글은 주재걸교수님의 인공지능을 위한 선형대수 강의를 듣고 정리한 내용입니다.
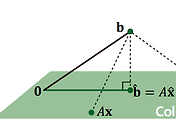
This can be viewed as a new linear system, 𝐶𝐱 = 𝐝, where a square matrix 𝐶 = 𝐴^𝑇𝐴 ∈ ℝ𝑛×𝑛 , and 𝐝 = 𝐴^𝑇𝐛 ∈ ℝ𝑛
If 𝐶 = 𝐴^𝑇𝐴 is invertible, then the solution is computed as

Another Derivation of Normal Equation

Computing derivatives w.r.t. 𝐱, we obtain

∵ x^T · a (=a^T · x) 를 미분한 값은 a가 된다. 순서를 바꿔서 한 내적이기 때문
Thus, if 𝐶 = 𝐴^𝑇𝐴 is invertible, then the solution is computed as

'Study > 선형대수학' 카테고리의 다른 글
| 3-5. 그람-슈미트 직교화와 QR 분해 (0) | 2022.01.04 |
|---|---|
| 3-4. Orthogonal Projection (0) | 2022.01.04 |
| 3-2 Least Squares와 그 기하학적 의미 (0) | 2022.01.03 |
| 3-1. Least Squares Problem (0) | 2022.01.01 |
| 2-6. 전사함수와 일대일함수 (0) | 2021.12.30 |
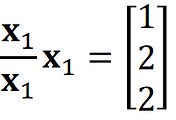
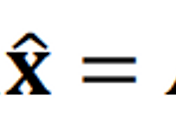
댓글