본 글은 Havard University Statistics 110 강의를 듣고 정리한 내용입니다.
확률론의 활용영역:
- 유전학, 물리학, 계랑경제학, 금융, 역사학, 정치
- 인문학, 사회과학계에서도 중요도와 활용이 늘어나고 있음
- 도박과 게임 - 통계에서 여러 번 연구된 주제이다(페르마, 파스칼)
- 인생 전반: (수학이 활실성에 대한 학문이라면,) 확률은 불확실성(uncertainty)을 계량화하는 것을 가능하게 해 준다.
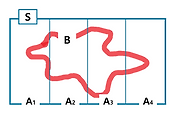
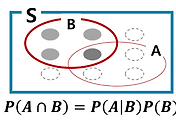
A sample space(표본 공간) is the set of all possible outcomes of an experiment
An event(사건) is a subset of the sample space
Naive definition of probability P(A) = Number of favorite outcomes / Number of possible outcomes (= #sample space)
- P : Probability
- A : event
- 모든 경우의 수가 fair 하다면 특정 케이스에 대한 probability 는 전체 케이스 갯수로 나눈 값이다.
- Assumes all outcomes equally likely finite sample space(동일한 probability를 가진다.)
Counting
- Multiplication Rule
- 첫 번째 사건에 대한 경우의 수가 n1, 두번째 사건에 대한 경우의 수가 n2 , ... , r번째 사건에 대한 경우의 수 nr
- overall possible outcomes = n1 * n2 * ... * nr
- Binomial coefficient nCk = n! / (n-k)!k!
- 순서 상관없이 n개중 k개를 고르는 방법의 갯수
- subset of size k
- number of group of people n
- Sampling table : choose k object out of n
Order matters Order doesn't Replace n^k n+k-1 C k Don't replace n*(n-1)*...*(n-k+1) n C k
'Study > 통계학' 카테고리의 다른 글
| 6. Monty Hall 문제와 심슨의 역설 (Monty Hall, Simpson's Paradox) (0) | 2022.01.18 |
|---|---|
| 5. 조건부 확률과 전확률정리 (Conditioning Continued, Law of Total Probability) (0) | 2022.01.17 |
| 4. 조건부 확률 (Conditional Probability) (0) | 2022.01.13 |
| 3. Birthday Problem과 확률의 특성 (Birthday Problem, Properties of Probability) (0) | 2022.01.13 |
| 2. 해석을 통한 문제풀이 및 확률의 공리 (Story Proofs, Axioms of Probability) (0) | 2022.01.11 |
댓글