본 글은 Havard University Statistics 110 강의를 듣고 정리한 내용입니다.
Sampling table : choose k object out of n
| Order matters | Order doesn't | |
| Replace | n^k | n+k-1 C k |
| Don't replace | n*(n-1)*...*(n-k+1) | n C k |
Pick k times from set of n objects, where order doesn't matter with replacement
- Extreme cases : k = 0 => n-1 C 0 = 1
- Less extreme cases : k = 1 => n C 1 = n
- Simplest nontrivial examples: n = 2 => k + 1 C k = k + 1 C 1 = k + 1
- 2개를 복원하여 k번 선택하는 경우의 수는 1번 물체를 0 ~ k번 선택하는 경우의 수와 같다.
- Equiv : k개의 구분 불가능한 입자를 n개의 구분가능한 박스 안에 넣는 경우의 수
- n = 4, k = 6, [***, ,**,*] -> ***||**|* -> 6(k)개의 *와 3(n-1)개의 |를 배열하는 경우의 수 = 6+3(n-1+k) C 6(k)
Story Proof(Proof by interpretation)
- Ex1. n C k = n C n-k
- Ex2. n * (n-1 C k-1) = k * (n C k)
- n명중 k명을 고르고 그중에서 1명을 대표로 선출하는 방법 = n명중 1명을 대표로 선출하고 n-1명중 k-1명을 고르는 방법
- Ex3. m + n C k = ∑(j = 0 ~ k) (m C j )* (n C k - j)
- m + n 명중 k 명을 고르는 방법 = m 명중 j 명을 뽑고, n명중 k-j명을 뽑는 방법들의 총 합
Non-Naive Definition
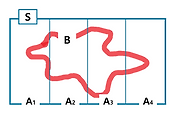
Probability sample contents of S and P where S is a sample space, and P(정의역은 S의 부분집합), a function which takes an event A⊆S as input, returns P(A)∈[0, 1] as outputs
- P(∮) = 0, P(S) = 1
- 공집합의 사건 발생 -> 일어나지 않는 사건이 발생 => 발생할 수 없음
- P(U An) = ∑P(An) if A1, A2, ... An are disjoint (non-overlap)
- both n = 1 ~ ∞
'Study > 통계학' 카테고리의 다른 글
| 6. Monty Hall 문제와 심슨의 역설 (Monty Hall, Simpson's Paradox) (0) | 2022.01.18 |
|---|---|
| 5. 조건부 확률과 전확률정리 (Conditioning Continued, Law of Total Probability) (0) | 2022.01.17 |
| 4. 조건부 확률 (Conditional Probability) (0) | 2022.01.13 |
| 3. Birthday Problem과 확률의 특성 (Birthday Problem, Properties of Probability) (0) | 2022.01.13 |
| 1. 확률과 셈 원리 (Probability and Counting) (0) | 2022.01.10 |
댓글