본 글은 Havard University Statistics 110 강의를 듣고 정리한 내용입니다.
Birthday Problem
특정 파티에 여러 사람이 있을 때, 같은 생일의 사람이 있을 확률에 대한 문제(최소 2명)
- K people, find prob that 2 habe same birthday
- 365 days a year(exclude Feb.29) equally likely, assume independent
- if k > 365, prob is 1 (pigeongole principle)
- Let k ≤ 365, prob > 0.5 일 경우 -> k = 23
- P(no match) = 365 * 364 * 363 * ... * (365 - k + 1) / 365^k
- P(match) =
- 50.7 % if k = 23
- 97 % if k = 50
- 99.999% if k = 100
- k C 2 -> 23 C 2 = 253
- 하루 다른 날도 같은 경우로 치는 경우 k = 14가 된다.
Properties(속성)
- P(A^c) = 1 - P(A)
- Proof : 1 = P(S) = P(A ∪ A^c) = P(A) + P(A^c) since A ∩ A^c = ∮
- if A ⊆ B(if A occer, than B occur), then P(A) ≤ P(B)
- Proof : B = A ∪ (B ∩ A^c), disjoint -> P(B) = P(A) + P(B ∩ A^c) ≥ P(A)
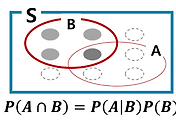
- P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
- Proof : P(A ∪ B) = P(A ∪ (B ∩ A^c))) = P(A) + P(B ∩ A^c) = P(A) + P(B) - P(A ∩ B) disjointification
- equiv to P(A ∩ B) + P(B ∩ A^c) = P(B)
- Proof : P(A ∪ B) = P(A ∪ (B ∩ A^c))) = P(A) + P(B ∩ A^c) = P(A) + P(B) - P(A ∩ B) disjointification
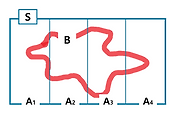
포함배제의 원리(Inclusion-exclusion Principle)
P(A ∪ B ∪ C) = P(A) + P(B) + P(C) - P(A ∩ B) - P(A ∩ C) - P(B ∩ C) + P(A ∩ B ∩ C)

deMontmort's Problem(1713)
1 ~ n 까지 표시된 카드 n장
뒤집은 가드에 표시된 숫자와 뒤집은 횟수가 같은 경우가 될 확률
P(Aj) = j번째 카드에 숫자 j가 써져있을 확률 = 1 / n since all position equally likely for card label j
P(A1 ∩ A2) = (n-2)! / n! = 1 / n(n-1)
- 카드 뭉치기의 순서는 n!
- 2장을 제외한 모든 카드는 자유롭게 배열 가능 ( n-2)!
P(A1 ∩ ... ∩ Ak) = (n-k)! / n!
∴P(A1 ∪ ... ∪ Ak) = n / 1! * 1 / n - n(n-1) / 2! * 1 / n(n-1) + n(n-1)(n-2) / 3! * 1 / n(n-1)(n-2) ...
≒ 1 - 1/2! + 1/3! - 1/4! + ,,, + (-1)^(n+1) * 1/n! = e^x 의 테일러급수 = 1 - 1/e
'Study > 통계학' 카테고리의 다른 글
| 6. Monty Hall 문제와 심슨의 역설 (Monty Hall, Simpson's Paradox) (0) | 2022.01.18 |
|---|---|
| 5. 조건부 확률과 전확률정리 (Conditioning Continued, Law of Total Probability) (0) | 2022.01.17 |
| 4. 조건부 확률 (Conditional Probability) (0) | 2022.01.13 |
| 2. 해석을 통한 문제풀이 및 확률의 공리 (Story Proofs, Axioms of Probability) (0) | 2022.01.11 |
| 1. 확률과 셈 원리 (Probability and Counting) (0) | 2022.01.10 |
댓글