6. Monty Hall 문제와 심슨의 역설 (Monty Hall, Simpson's Paradox)

본 글은 Havard University Statistics 110 강의를 듣고 정리한 내용입니다.

 

Monty Hall Problem

1 door has car, 2 doors have goats, Monty knows which

Monty는 항상 염소가 있는 문을 연다. (Monty가 2번 문을 열었다 -> 2번 문 뒤에 염소가 있음을 가정.)

바꾸는게 좋을 것인가?

2번 문을 여는 조건부 확률

P(success if switch | Monty opens door 2) = 2/3

 

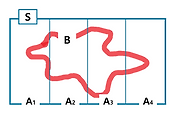
Law of total probability

wish we knew where car is

event S : succeed (assuming switch)

event Dj : Door j has car(c ∈ (1, 2, 3))

P(S) = P(S|D1) / 3 + P(S|D2) / 3 + P(S|D3) / 3

 = 0 + 1 * 1/3 + 1 * 1/3 = 2/3

 

Simpson's Paradox

Hibbert : 80%, Nick : 83%

Nick은 쉬운 수술을 훨씬 많이함. 단순 확률로만 보면 Nick이 더 훌륭한 의사처럼 보이지만, 수술 종류별 성공률을 보았을때, Hibbert가 더 좋은 의사임이 분명함

 

event A : successful surgery

event B : treated by doctor Nick

event C : heart surgery

 

• P(A|B,C) < P(A|B^c,C)
• P(A|B,C^c) < P(A|B^c,C^c)
• but P(A|B) > P(A|B^c)

C is a confounder(교란변수), 적절한 confounder에 대한 조건부 확률을 확인하지 않으면 잘못된 판단을 내릴 수 있다.

 

전체 확률의 정의를 이용해 심슨의 역설이 틀렸음을 증명할 수 있는가?

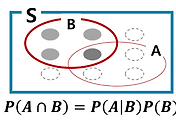
P(A|B) = P(A|B,C)P(C|B) + P(A|B,C^c)P(C^c|B)에서 

P(A|B,C) < P(A|B^c,C), P(A|B,C^c) < P(A|B^c,C^c)는 확인 가능하지만 P(C|B), P(C^c|B)가 좌항, 우항에 서로 다른 가중치로 작용하기 때문에 증명할 수 없다.

 

 

출처: https://www.edwith.org/ai152