본 글은 Havard University Statistics 110 강의를 듣고 정리한 내용입니다.
Gambler's Ruin
Two gamblers A and B sequence of rounds bet $1, p = P(A wins a certain round), q = 1-p
Find prob that A wins entire game (so B is ruined)
assuming A starts with $i, B starts with %N-i

p_i = P(A wins game | A starts at $i) = p*p_i+1 + q*p_i-1, 1 ≤ i ≤ N-j, p_0 = 0. p_N = 1
계차방정식(difference equation) -> 미분 방정식의 이산형태
guessing을 통한 풀이
Guess p_i = x^i

p≠q일 경우,

p=q일 경우,

ex. i = N-i, p = 0.49일 때,
- N = 20 => 0.40
- N = 100 => 0.12
- N = 200 => 0.02
Random Variable
A function from sample space S to R

Bernoulli
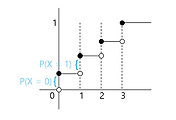
- 확률변수 x가 베르누이 분포를 따른다는 것은 x가 0과 1 두 값만 가질 수 있다는 것이다.
- Bern(p)
- P(X=1) = p, P(X=0) = 1-p
Binomial(n, p)
- n개의 독립적인 Bern(p)의 성공 횟수의 분포
- Bin(n, p)
- PMF(확률질량함수) P(X=k) = n C k p^k (1-p)^(n-k)
- X ~ Bin(n, p), Y ~ Bin(m, p) indep Then X + Y ~ Bin(n+m, p)
'Study > 통계학' 카테고리의 다른 글
| 9. 기댓값, 지시확률변수와 선형성 (Expectation, Indicator Random Variables, Linearity) (0) | 2022.01.22 |
|---|---|
| 8. 확률변수와 확률분포 (Random Variables and Their Distributions) (0) | 2022.01.20 |
| 6. Monty Hall 문제와 심슨의 역설 (Monty Hall, Simpson's Paradox) (0) | 2022.01.18 |
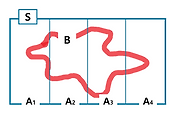
| 5. 조건부 확률과 전확률정리 (Conditioning Continued, Law of Total Probability) (0) | 2022.01.17 |
| 4. 조건부 확률 (Conditional Probability) (0) | 2022.01.13 |

댓글