본 글은 Havard University Statistics 110 강의를 듣고 정리한 내용입니다.
Binomial distribution X ~ Bin(n, p)
n = 정수, p = 0~1 실수
- Story : X is number of success in n independent Bern(p) trial
- Sum of indicator rvs(지표 확률 변수) : X = X1 + X2 + ... + Xn, Xj = {1 if jth trial success, 0 otherwise}
- X1, ..., Xn i.i.d Bern(p) (independent identically distribution)
- PMF P(X=k) = nCk p^k q^(n-k)
- ∑ nCk p^k q^(n-k) = (p+q)^n = 1 (이항 정리)
R.V.S
- S = {7,7,5,5,5,3,3,3}
- X = 7 is an event
- X ≤ x is an event
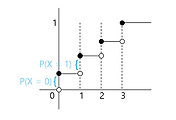
- F(x) = P(X≤x) then F is the CDF(누적분포함수) of X
PMF(확률질량함수) (for discrete r.v.s)
discrete : possible values a1, a2, ... ,an or ∞
- P(X=aj) = pj for all j
- condition for PMF pj ≥ 0 , ∑ pj = 1
X ~ Bin(n, p), Y ~ Bin(m, p) indep Then X + Y ~ Bin(n+m, p)
- inndediate from story(동전던지기)
- 같은 정의역을 가져야 더할 수 있다
- 성공확률이 같아야 한다
- X = X1 + ... + Xn, Y = Y1 + ... + Yn => X + Y = ∑Xi + ∑Yj
- sum of n+m i.i.d Bern(p) => Bin(n+m, p)
- Use PMF, P(X + Y = k) = ∑[j = 0~k] P(X+Y=k|X=j)P(X=j) = ∑P(Y=k-j|X=j) n C j p^j q^(n-j)
위 식은 X와 Y가 독립이라는 조건 때문에 ∑P(Y=k-j) n C j p^j q^(n-j) 로 바꿀 수 있다.
∑ m C (k-j) p^(k-j) q^(n-k+j) n C j p^j q^(n-j)
= p^j q^(m+n-k) ∑ m C (k-j) n C j (발데르몽드) = (m+n) C k => PMF of Bin(n+m, k)-> 이항정리
Ex. Choose 5 card, find distribution of #aces (PMF or CDF). Let X = (#aces)
Find P(X=k) k ∈ {0, 1, 2, 3, 4}인 경우가 아니면 모두 0, Not Binomial -> 각 시행이 독립이지 않기 때문

Like the elk problem

- b개의 검정색 구슬과 w개의 흰색 구슬 중에서 n개의 표본을 무작위로 추출할 때, 표본에 있는 흰색 구슬의 수

Hypergeometric(초기하분포)
- sampling without replacement
- 이항분포와 크게 차이나지 않는 경우(ex. 100만개 중 2개를 뽑는 경우)는 초기하분포가 이항분포에 근사한다.
- 유효한 확률질량함수인지 확인



출처: https://www.edwith.org/ai152
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=mykepzzang&logNo=220836321999
'Study > 통계학' 카테고리의 다른 글
| 10. 기댓값 (Expectation Continued) (0) | 2022.01.24 |
|---|---|
| 9. 기댓값, 지시확률변수와 선형성 (Expectation, Indicator Random Variables, Linearity) (0) | 2022.01.22 |
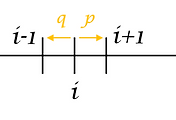
| 7. 도박꾼의 파산 문제와 확률변수 (Gambler's Ruin and Random Variables) (0) | 2022.01.20 |
| 6. Monty Hall 문제와 심슨의 역설 (Monty Hall, Simpson's Paradox) (0) | 2022.01.18 |
| 5. 조건부 확률과 전확률정리 (Conditioning Continued, Law of Total Probability) (0) | 2022.01.17 |

댓글