본 글은 Havard University Statistics 110 강의를 듣고 정리한 내용입니다.
Proof Linearity
Let T = X + Y, show E(T) = E(X)+E(Y)
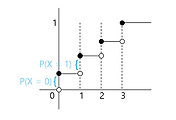
E(T) = ∑ tP(T=t) ?= ∑ xP(X=x) + ∑ yP(Y=y)
- P(T=t) = ∑P(T=t|X=x)P(X=x)

평균을 구하는 방법은
- 전부 더해서 나누는 방법 ∑X(s)P({s}), P({s}) = 조약돌의 무게 = 1/n
- 그룹으로 묶어서 가중평균을 구하는 방법이 있다. ∑xP(X=x)
Proof of linearity(discrete case)
- ∑(X+Y)(s)P({s}) = ∑(X(s)+Y(s))P({s}) = ∑X(s)P({s}) + ∑Y(s)P({s}) = E(X)+E(Y)
- E(cx) = cE(x) if c is const
- if X = Y -> E(X+Y) = E(2X) = 2E(X) = E(X)+E(Y)
Negative Binomial
parameters r, p
Story : indep Bern(p) trials, number of failures before the rth success
1000100100001001 -> r = 5, n = 11 zeros(failures)
- PMF : P(X=n) = n+r-1 C r-1 p^r (1-p)^n
- E(X) = E(X1+...+Xr) = E(X1) + ... + E(Xr) = rq/p
- Xj is number of failures between j-1st and jth success, Xj ~ Geom(p)
첫 번째 성공까지 걸린 시도 수 'First Success' 분포: X ~ FS(p)
Let Y = X-1(마지막 성공한 횟수는 제외), then Y ~ Geom(p), E(X) = E(Y)+1 = q/p + 1 = 1/p
Putnam Problem
Random Permutation of 1,2,...,n, where n ≥ 2
Find excepted number of local maxima, {3,2,1,4,7,5,6} -> 2 local maxima and 1 global maxima
- Let I_j be indicator r.v. of position j having a local max, 1 ≤ j ≤ n -> I_j = number of local max
- 위 예시에서 4, 7, 5 를 보게 되면 여기서 가장 큰 값이 중앙에 올 확률은 1/3 -> 3개씩의 위치에서 각각 1/3 이므로 (n-2)/3
- local minima는 끝 2개에 존재하고, 바로 옆의 수보다 클 확률이기 때문에 2 * 1/2 가 된다.
- E(I_1) + E(I_2) + ... + E(I_n) = (n-2)/3 + 2/2 = (n+1)/3
- n=2인 경우 1,2 2,1두가지 이기 때문에 기댓값은 1이다.(3/3 = 1)
St.Petersburg Paradox
동전의 앞면이 나올때까지 계속 던져서 앞면(H)이 나올 때까지 던진 횟수 x의 $2^x를 받는다. (성공횟수 포함)
이 게임을 위해 얼마나 내야 하는가?
Y = 2^x, find E(Y)
E(Y) = ∑[k=1~∞] 2^k * 1/(2^k) = ∑[k=1~∞] 1 = 1+1+.... = ∞
$1조 = $2^40 로 돈의 제한을 걸게 되면, ∑[k=1~40] 1 = 40
∴ ∞ = E(2^x) != 2^E(X) = 4
첫 성공의 기댓값은 1/p(negative binomial) 이기 때문에 2^E(X)는 4가 된다.
'Study > 통계학' 카테고리의 다른 글
| 12. 이산, 연속, 균등분포 (Discrete vs. Continuous, the Uniform) (0) | 2022.01.27 |
|---|---|
| 11. 포아송분포 (The Poisson distribution) (0) | 2022.01.25 |
| 9. 기댓값, 지시확률변수와 선형성 (Expectation, Indicator Random Variables, Linearity) (0) | 2022.01.22 |
| 8. 확률변수와 확률분포 (Random Variables and Their Distributions) (0) | 2022.01.20 |
| 7. 도박꾼의 파산 문제와 확률변수 (Gambler's Ruin and Random Variables) (0) | 2022.01.20 |



댓글