본 글은 Stanford University CS231n 강의를 듣고 정리한 내용입니다.
Activation Functions

input으로 들어온 데이터를 weight와 곱해주고, activation function을 통과하는 과정을 거친다.

Sigmoid


Problem of Sigmoid
1. Saturated neurons 'kill' the gradients

x = -10 -> gradient는 0에 가까운 값이 된다.
x = 0 -> resonable gradient를 얻게 되어 역전파가 잘 일어난다.
x = 10 -> gradient는 0에 가까운 값이 된다.
2. Sigmoid outputs are not zero-centered

neuron의 입력 x가 항상 양수라면 W의 값들을 항상 증가시키거나 항상 감소시키는 등 한 방향으로만 업데이트가 진행되게 된다.

W가 2-dim인 예시인데, 이 경우 4개의 사분면 중 둘다 positive 혹은 negative인 두개의 사분면의 방향으로만 업데이트가 이루어지게 된다. optimal W를 찾는 과정에 빨간색 화살표와 같이 허용된 방향으로만 optimal 값을 찾아 나가게 된다. 이러한 문제를 방지하기 위해 mean이 0에 가까운 데이터를 얻기를 원한다.
3. exp() is a bit compute expensive
연산 량이 많으나 major problem은 아니다.
Tanh

ReLU(Rectified Linear Unit)

Positive Things
- Does not saturate(in + region)
- Very computationally efficient(exp와 같은 연산이 없다)
- Converges much faster than sigmoid/tanh in practive(약 6배 빠름)
- Actually more biologically plausible than sigmoid
ReLU는 2012년 AlexNet에서 본격적으로 사용되기 시작했다.
Problems
- Not zero-centered output
- sigmoid에서 가지고 있던 문제를 tanh에서 해결하였으나, ReLU에서 다시 발생하였다.
- An annoyance
- positive에서는 saturate가 일어나지 않지만, 반대로 negative에서는 saturate가 발생한다.
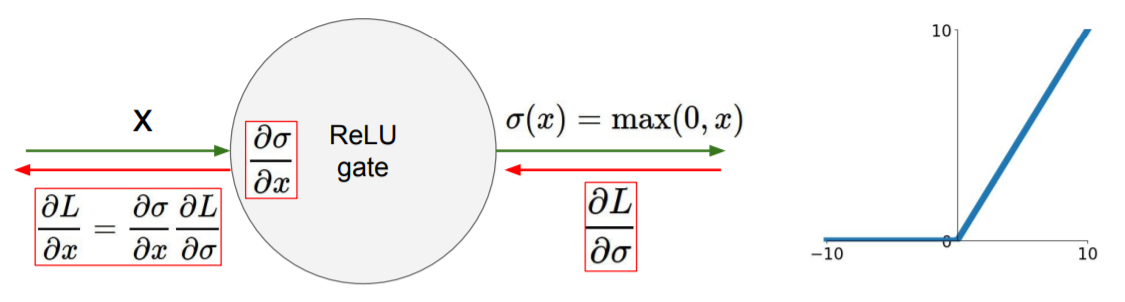
x = -10 -> gradient = 10
x = 0 -> gradient = 0
x = 10 -> gradient = 0
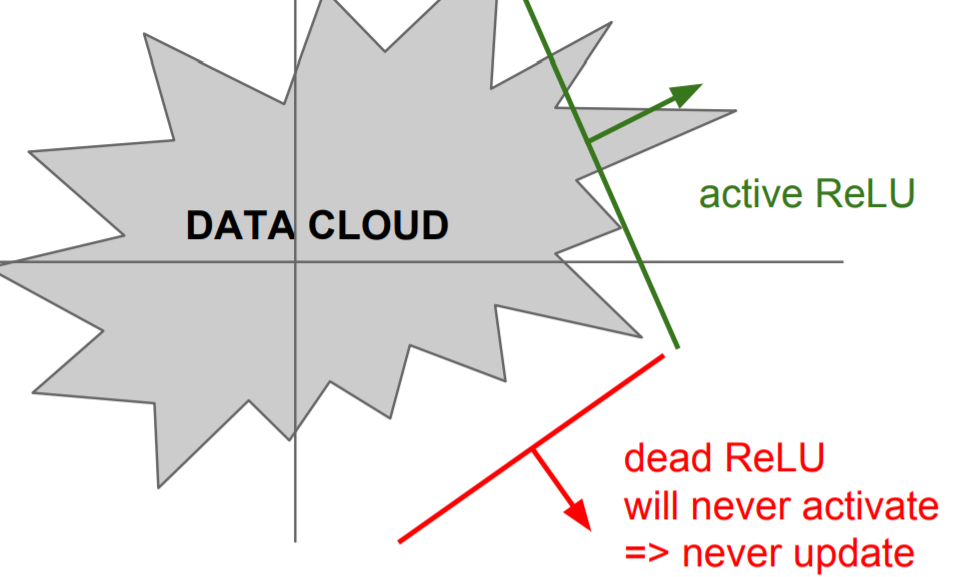
- Initialization을 잘못한 경우, dead ReLU 부분에 가게 되어 activate되지 않는다.
- learning rate가 매우 큰 경우, weight가 크게 뛰어 data manifold에서 벗어나게 된다.
=> 사람들은 ReLU neuron들을 아주 작은 positive biases로 initialize 하려한다. (e.g. 0.01)
Leaky ReLU
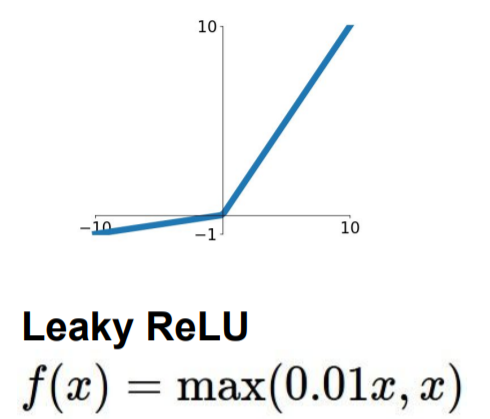
Positive Things
- Does not saturate
- Very computationally efficient(exp와 같은 연산이 없다)
- Converges much faster than sigmoid/tanh in practive(약 6배 빠름)
- Will not "die"

backprop하고 학습을 하는 과정을 통해 parameter인 alpha값을 정함으로써 Leaky ReLU에 비해 약간의 유연성이 더 주어진다.
ELU(Exponential Linear Units)
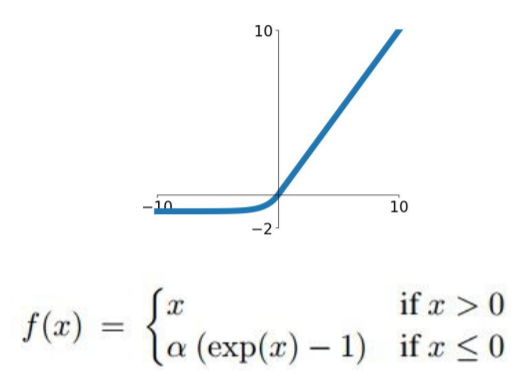
Positive Things
- All benefits of ReLU
- Closer to zero mean outputs(benefits of Leaky ReLU or Parametric ReLU)
- 음수부분에 saturate되는 부분이 있어 Leaky ReLU에 비해 노이즈에 대하여 robust하다
Problems
- exp 연산이 요구된다.
Maxout
dot product 후 nonlinearity 식에 넣는 일반적인 형태를 가지지 않는다.
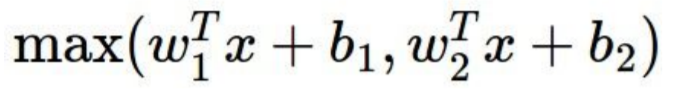
Positive Things
- Generalizes ReLU and Leaky ReLU
- Linear Regime
- Dose not saturate
- Dose not die
Problems
- parameter와 neuron의 수가 두배가 된다.
Summary
- ReLU를 사용한다. 그러나 learning rate를 주의해야 한다.
- Leaky ReLU, Maxout, ELU를 시험해본다
- tanh를 시험해보나 많이 기대하지 마라
- sigmoid를 사용하지 마라
Data Preprocessing
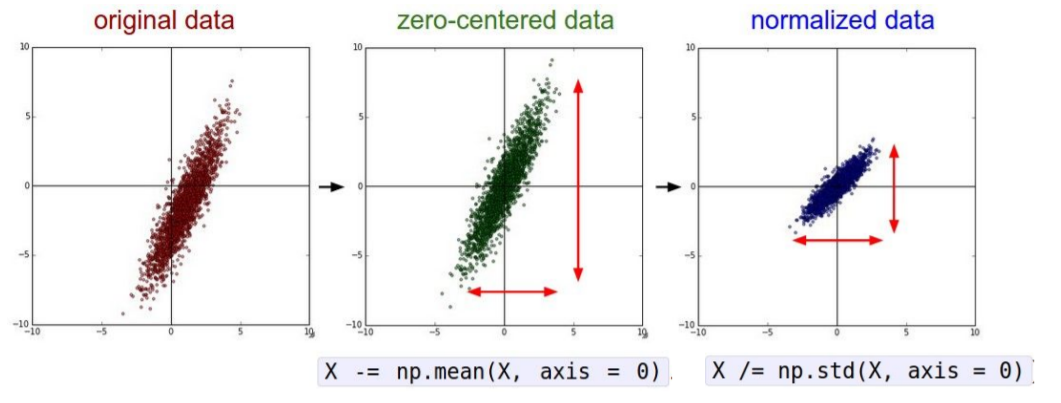
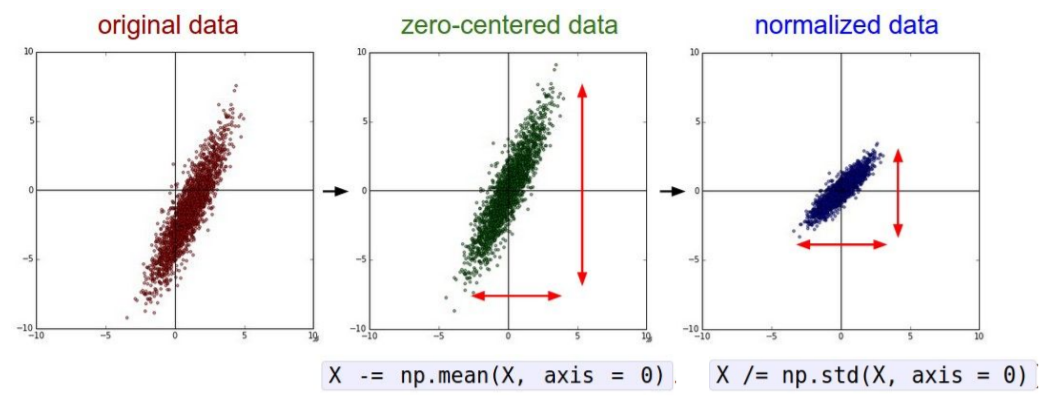
위 과정을 진행하는 이유는 앞서 봤던 data가 전부다 양수인 경우 weights가 모두 양수가 될 것이고, suboptimal optimization을 얻게 된다.
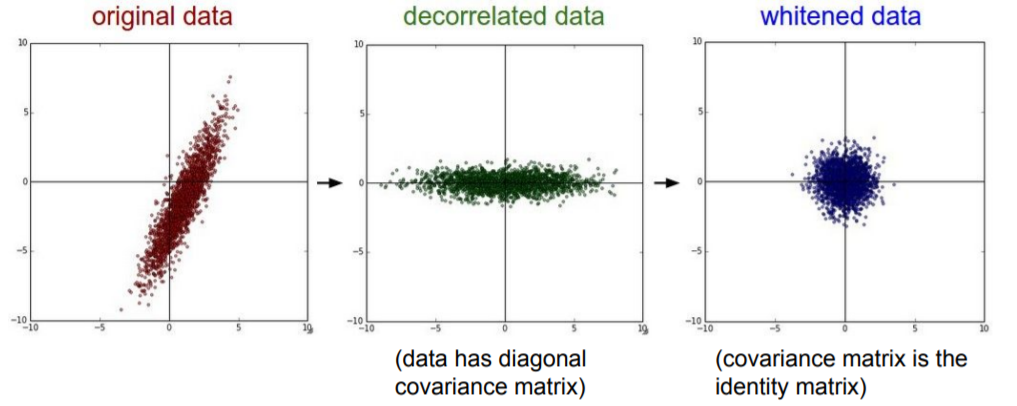
하지만 일반적으로 이미지의 경우에는 픽셀들을 너무 많이 정규화할 필요가 없다. 왜냐하면 이미지는 각 위치에서 이미 비교적 비슷한 규모와 분포(0~256)를 가지고 있기 때문이다. 따라서 zero-centering 정도만 해주면 충분하다. 우리는 전형적으로 convolutional networks를 공간적으로 적용해서, 원본 이미지 위에서 공간 정보를 포함한 형태로 특징을 추출해낸다.
Summary
[32, 32, 3]인 CIFAR-10 이미지를 다룬다고 할 때
- 이미지의 mean을 subtract한다.(e.g. AlexNet)
- 각 채널별 mean을 subtact한다(e.g. VGGNet)
Weight Initialization
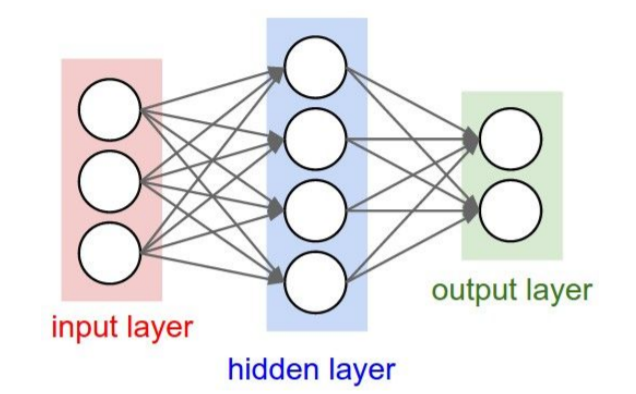
Q: 모든 파라미터가 0이면(W=0) 어떻게 되는가?
A: 모든 neuron이 죽지는 않으나 똑같은 행동을 반복하기 때문에 모든 output이 같고, 결국 모든 gradient가 같아진다.
First idea: Small random numbers
평균이 0 표준편차가 0.01이도록 해준다.

작은 network에는 효과적이나 deep network에는 좋지 않다.
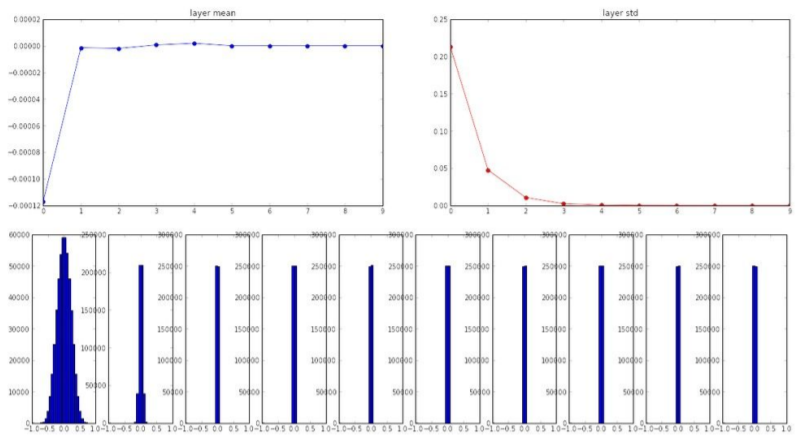
첫 레이어에는 평균이 0에 가깝고 적당한 표준편차를 가지는 것이 보이나, 뒤로갈수록 표준편차가 0으로 빠르게 가는 것을 확인할 수 있다. -> 모든 activations이 0이 된다.
Q. What do the gradients look like?
A. 입력값이 매우 작다. weight에 대한 gradient는 upstream gradient * local gradient이다. 이 dot product는 W x X를 수행하는데, 기본적으로 X가 된다. 바로 입력값이다. 따라서 X가 작기 때문에 가충치는 매우 작은 기울기를 얻게 되고, 업데이트 되지 않는다.
표준편차가 0.01 대신에 1이 되도록 해주는 경우
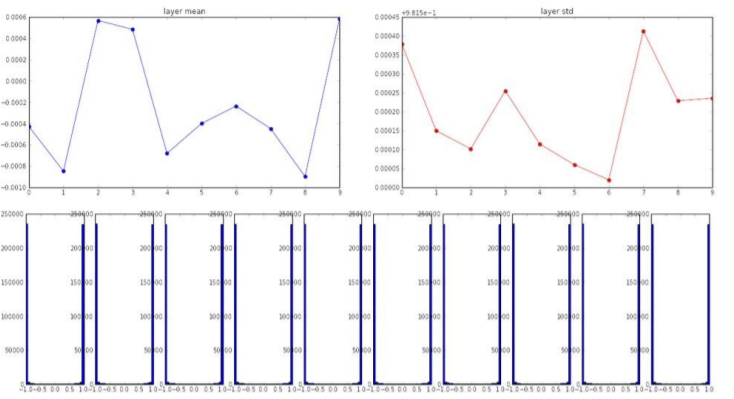
모델에서 tanh를 통과하기 때문에 saturated 된다. 가중치가 너무 커서 distribution of activation이 -1이나 1의 값만 가진다.
Xavier Initialization

Standard gaussian으로 얻은 sample을 input의 갯수로 scale해준다. input와 output의 노드 갯수로 W를 결정하게 되는데, input의 갯수가 적으면 작은 수로 나누기 때문에 같은 larger variance at output에 대해서 더 큰 Weight를 가지게 된다.
그러나 ReLU와 같은 비선형 case에는 적절하지 않은데, ReLU의 특성을 생각해보면 음수인 경우 모두 가중치가 0이었기 때문에 기울기도 반토막이 된다. 따라서 비선형 case에 대해서는 he 초기값을 사용한다.

Batch Normalization
일부 레이어에서 activation의 batch를 고려한다. 각 dimension의 unit을 가우시안으로 만들기 위해 아래 식을 이용한다.
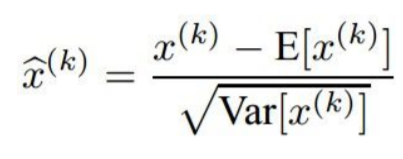
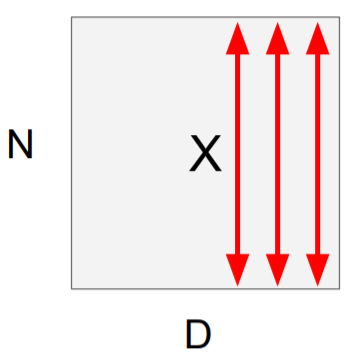
1. empirical mean(경험적 평균)과 분산을 각 dimension마다 독립적으로 계산한다.
2. Normalize
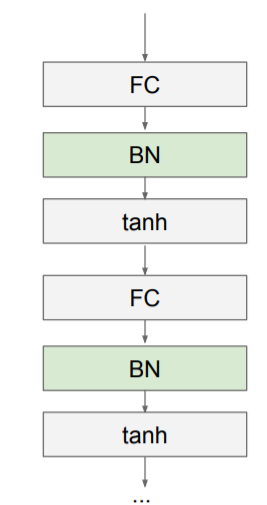
주로 Fully Connected layer나 Convolutional layer 뒤에 그리고 nonlinearity 앞에 삽입된다.
layer에서 W와의 곱셈 연산을 진행하기 때문에, 여러번 진행하다 보면 bad scaling effect를 가지게 된다. BN은 기본적으로 이 effect를 없애기 위함이다.
Problem: do we necessarily want a unit gaussian input to a tanh layer?
초기값을 설정하는데 많은 공을 들이지 않고도 활성화값 분포를 적당히 퍼트릴 수 있도록 강제할 수 있다는데 이점이 있다.


- network에서의 gradient flow를 향상시킨다.
- 더 넓은 범위의 learning rate를 허용한다.
- initialization에 대한 의존성이 낮아진다.
- dropout의 필요성을 낮춰줄 수 있다.
- batch size가 작은 강화학습 같은 경우에는 덜 accurate하나 효과가 있는것은 같다.
Q) tanh layer에는 반드시 가우시안 단위의 입력이 필요한가?
"saturated를 어떻게 처리할 것인가"라는 점에서 그렇다. 정규화 후 네트워크는 학습을 통해 범위를 축소할 수 있다. 감마와 베타는 모두 매개변수(parameter)다. To be learned, gamma is scaling and beta is shifting. (BN just scaling and shifting. It does not change structure.) 이것들은 BN이 작동하는 방식에 유연성을 부여하는데 사용된다.
Babysitting the Learning Process
Step1. preprocess the data
Step2. Choose the architecture
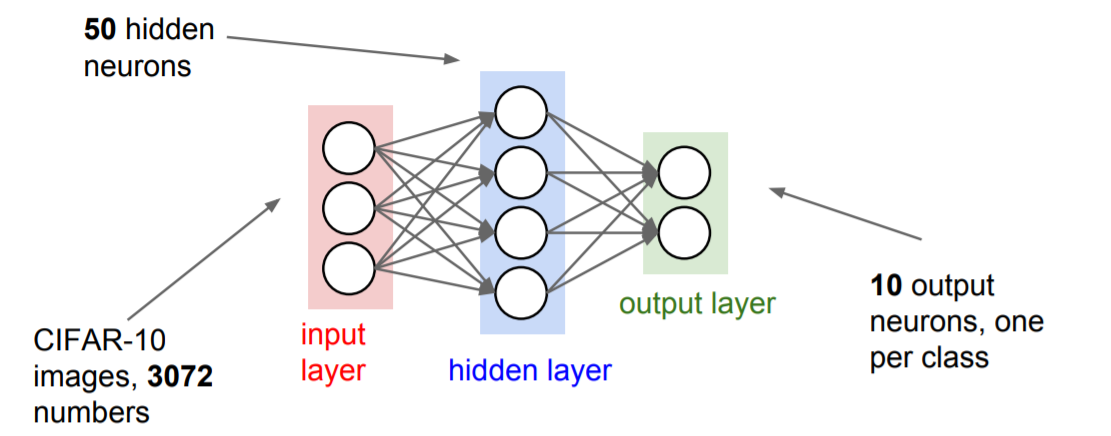
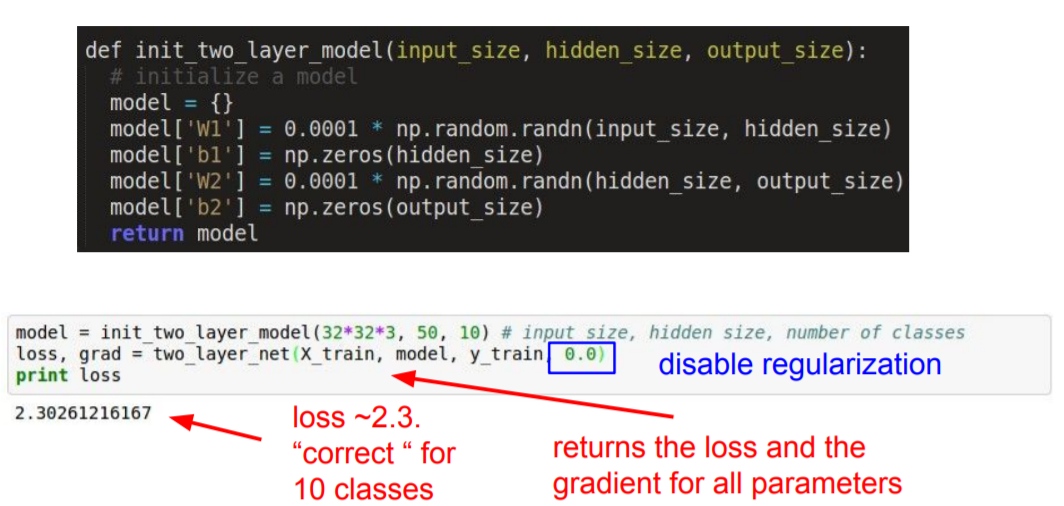
우리가 만든 loss가 resonable한지 확인해야 한다. Softmax classifier를 사용한다고 가정한다. W가 작고 일반적으로 분산분포(diffuse distribution)을 가지고 있을 때, Softmax classifier loss는 1~10의 negative log 가 될 것이고, regularization 값을 0으로 했을 때 이 값이 여기서는 2.3이 나왔다.
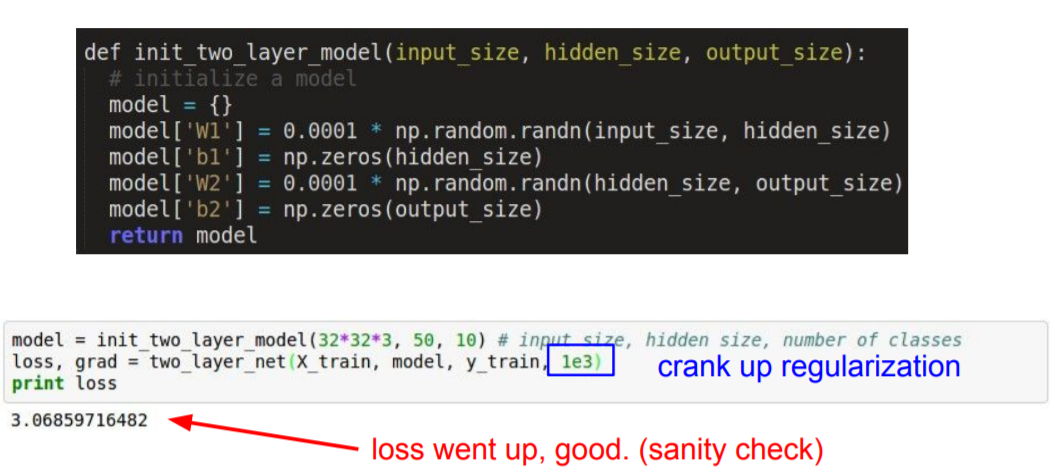
regularization 값을 살짝 올렸을 때, loss 값이 올라간걸 확인할 수 있다. 이러한 방식으로 layer의 동작을 확인하는 것이 sanity check이다
Step3. Training

적은 data로 학습하게 되면 overfitting이 일어나기 때문에, 적은 데이터로 loss가 0으로 가는지 확인해본다.
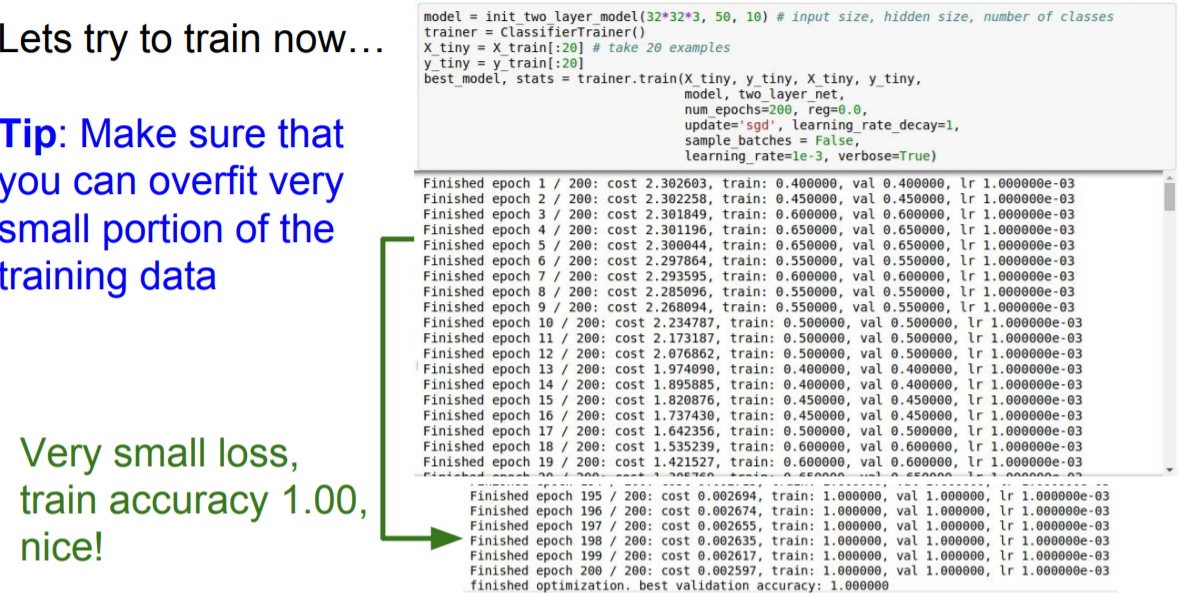
loss값이 매우 작고, train acc가 1이므로 sanity check이 되었다.


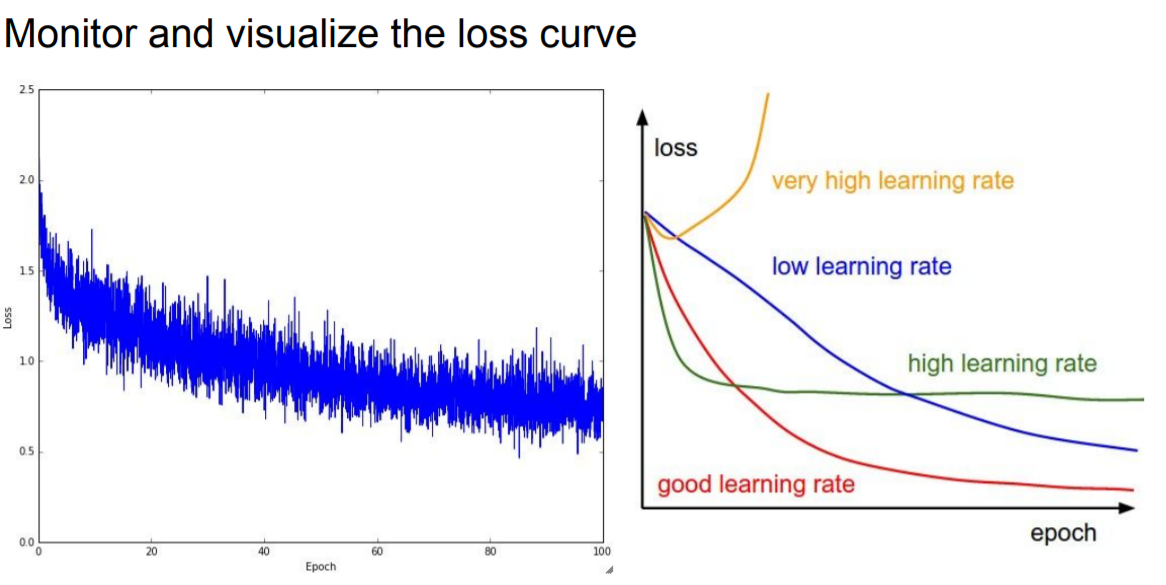
learning rate가 너무 작으면 loss의 변화량이 매우 적다. 반대로 learning rate가 매우 크면 NaN값이 나오게 된다.
적정 범위는 [1e-3 ... 1e-5]정도가 된다.
Hyperparameter Optimization
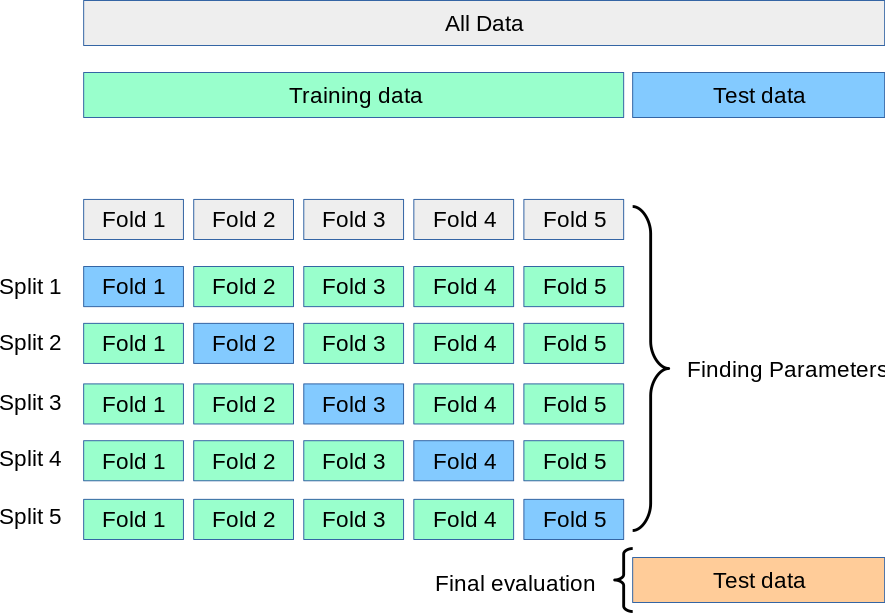
Cross-validation strategy
- First stage: 몇번의 epoch만 반복해서 parameter가 작동하는지 확인
- Second stage: longer running time, finer search
만약 cost가 original cost의 3배보다 커지는 경우 early break 하게 된다.
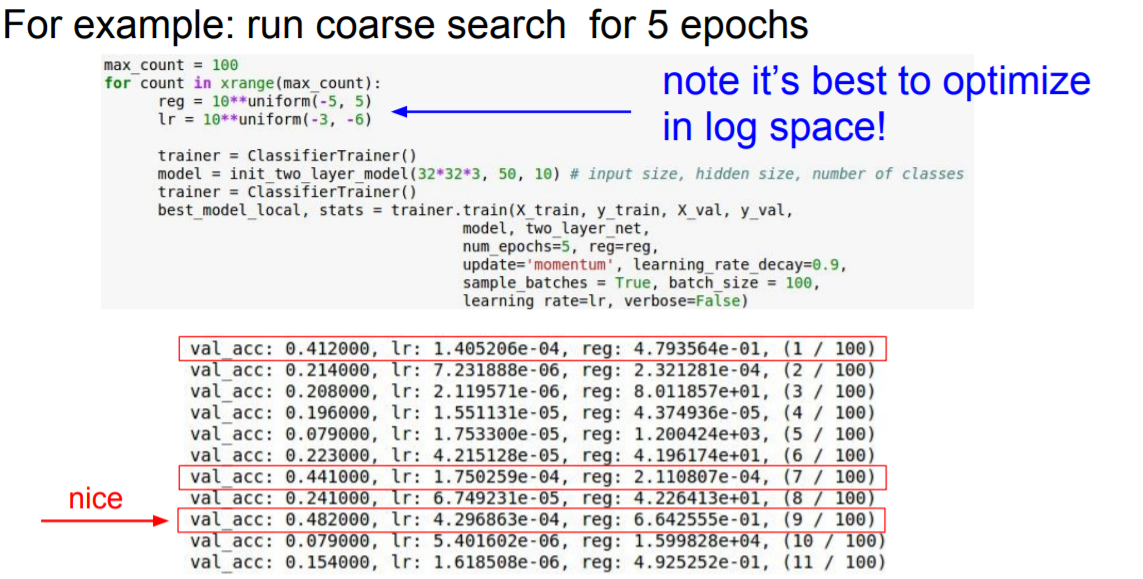
validation acc값이 높게 나온 경우를 살펴보면, learning rate값이 1e-3~1e-4정도의 값을 가지는 것을 확인할 수 있다. 10번의 epoch로 나온 결과를 통해 lr값의 범위를 수정해준다.

best case를 보게 되면 learning rate가 1e-3에 거의 근접한 값을 가지는 것을 볼 수 있다. best case에 해당하는 parameter값은 전체 범위의 중간정도에 해당하게 설정하는 것이 가장 좋다.
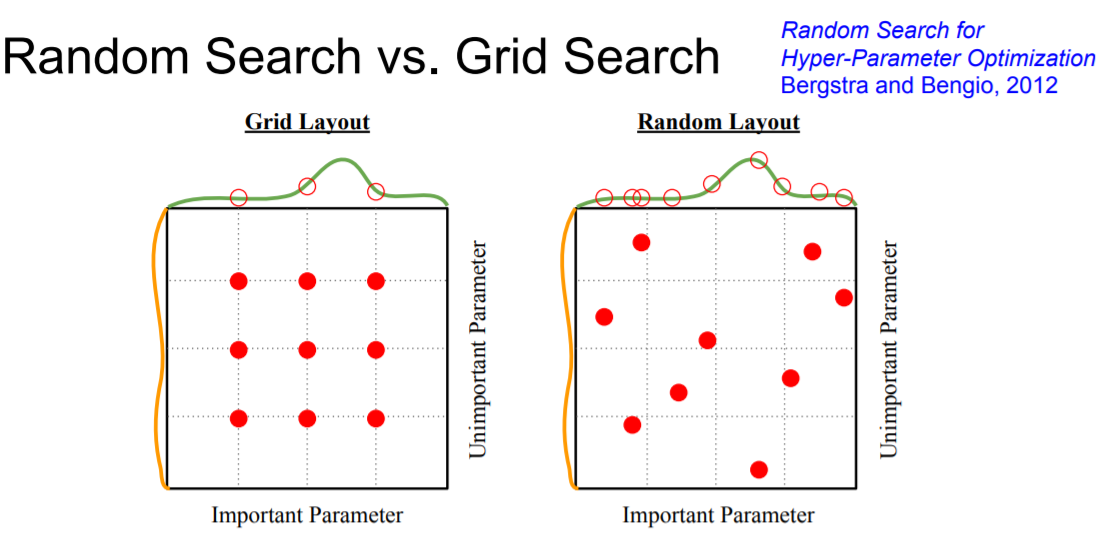
Hyperparameter값을 찾는 방법은 Grid search와 Random search가 있는데, 위 그림에서 보듯이 Grid search는 최적의 값을 찾지 못할수도 있다. 이 경우는 Random Search가 더 좋은 방법이다.
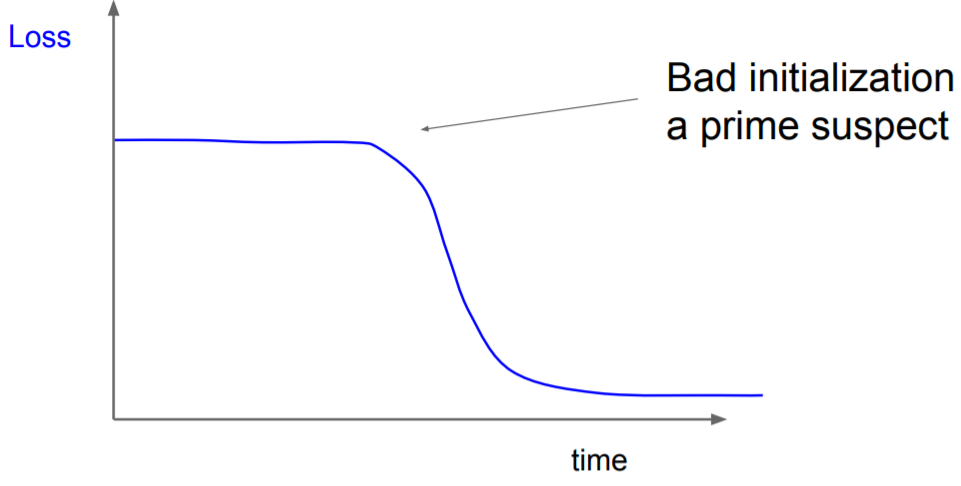
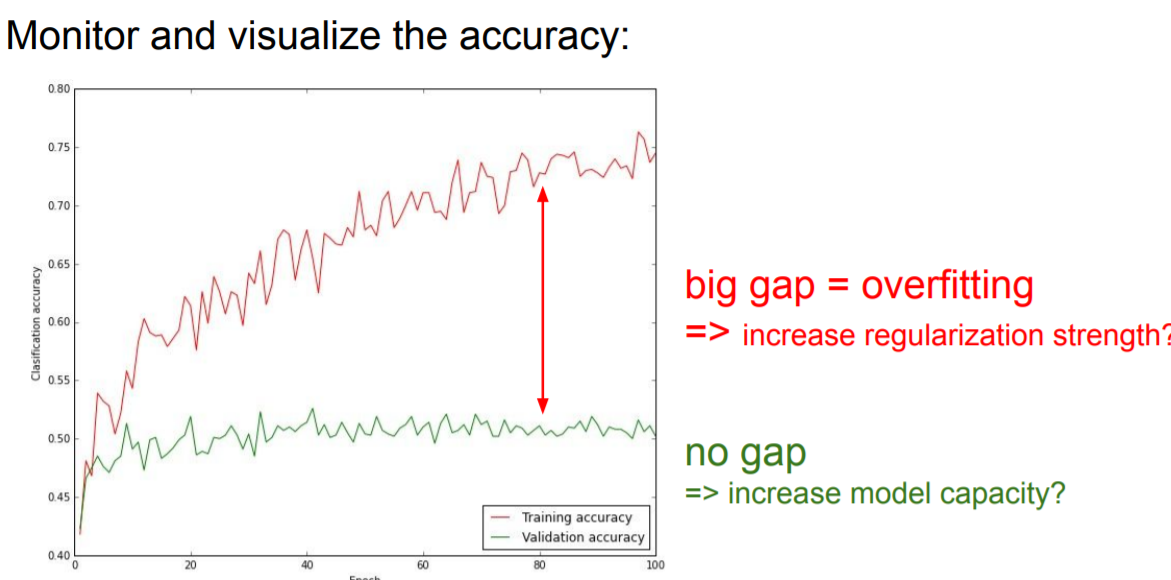
출처: http://cs231n.stanford.edu/2017/index.html
https://say-young.tistory.com/entry/CS231n-Lecture-6-Training-Neural-Networks-I
'Study > CS231n' 카테고리의 다른 글
| Lecture 7 . Training Neural Networks II (0) | 2022.02.14 |
|---|---|
| Lecture 5. Convolutional Neural Networks (0) | 2022.01.21 |
| Lecture 4. Introduction to Neural Networks (0) | 2022.01.13 |
| Lecture 3. Loss Functions and Optimization (0) | 2022.01.11 |
| Lecture2. Image Classification (0) | 2022.01.10 |




댓글