본 글은 Stanford University CS231n 강의를 듣고 정리한 내용입니다.
Loss Function : 학습 진행 과정에서 W값이 얼마나 나쁜지를 나타내 주는 함수
Optimization : 모든 가능한 W들 중에 가장 덜 나쁜(bad) W를 찾는 과정


image x와 weight W를 통해 나온 결과와 label y간의 loss값을 모두 더한 뒤 데이터의 갯수만큼 나눠준 값
loss값을 최소화 하는 W값을 찾아가는 과정이 필요함
CIFAR-10의 경우 10개의 class가 있기 때문에 맞고 틀린게 아닌 multiclass에 대한 계산이 필요하다.
Multiclass SVM Loss


정답 class의 score가 다른 label의 score보다 월등히 큰 경우(위 식에서는 1이상 큰 경우)에는 loss값을 0으로 간주한다.


Q1. What happens to loss if car scores change a bit?
A : Car score는 이미 다른 class의 score보다 충분히 크기 때문에 loss의 값은 변하지 않는다.
Q2. What is the min/max possible loss?
A : minimun = 0, maximun = ∞
Q3. At initialization W is small so all s ≈ 0. What is the loss?
A : Number of classes minus one
위 예시에서 고양이 사진에 대한 loss는 max(0, 0-0+1)이기 때문에 모든 경우에 1이 나오게 되고, 이를 합하면 클래스당 2가 나온다. 2는 결국 Number of class - 1의 값이 된다.
sanity check : 초기에 위 과정을 진행하여 학습을 진행해도 되는지의 여부를 확인하는데 사용한다.
Q4. What if the sum was over all classes? (including j = y_i) (y_i와 j가 같은 경우는 원래 sum을 하지 않지만, 이경우까지 전부 sum을 한다면 어떻게 되는가?)
A : loss increases by one
y_i와 j가 같은 경우 max(0, sj - syi + 1)의 값이 1이 되기 때문에 loss값이 각 클래스마다 1 늘어나고, 전체에 대해서도 1 증가하게 된다.
Q5. What if we used mean instead of sum?
A : Doesn't change
Q6. What if we used Li = ∑max(0, sj - syi + 1)^2 ?
A : Different, linear 하지 않기 때문
조금의 변화에도 많이 좋아진 것 처럼 나타날 수 있다.

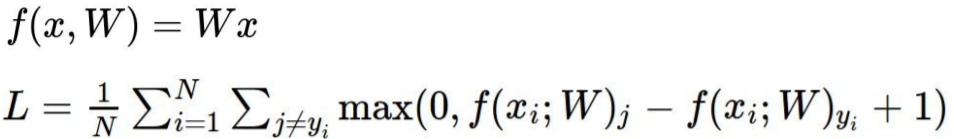
Q7. Suppose that we found a W such that L = 0. Is this W unique?
A : W는 unique하지 않음, 2W also has L = 0
SVM의 경우 loss function이 train data에 초점을 맞추고 있지만, 현실에서는 test data에 대한 정확도를 신경써야 하기 때문에, training data performance는 그닥 중요하지 않다.
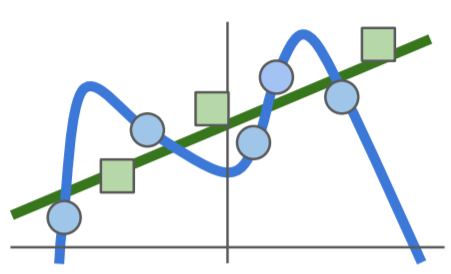
파란 선의 경우 training data에는 좋은 성능을 보이나, test data에 대해서는 하나도 맞추지 못한다. 이러한 선 보다는 초록색의 선이 training data와 test data 모두에 대해 어느정도의 정확도를 보인다.

Regularization

L2 regularization은 보다 robust한 regularization을 제공해준다.

If you are a Bayesian: L2 regularization also corresponds MAP inference using a Gaussian prior on W
Softmax
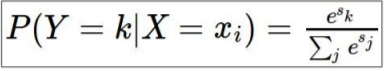
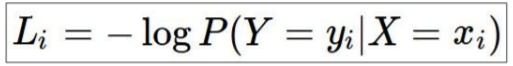
log 함수는 값이 커질수록 커지는 함수이나, loss 함수는 값이 클수록 좋지 않음을 나타내기 때문에 positive가 아닌 negative로 나타낸다.

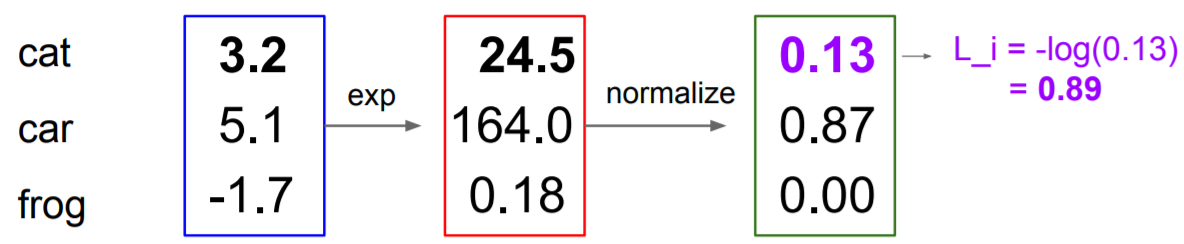
score값을 구한후, 이를 exponential 해주고 이 값을 normalize 해준다. 결과값을 -log 취해주면 loss 값이 나오게 된다.
Q1. whst is the min/max possible loss L_i ?
A. min = 0, max = ∞
정답에 모든 score가 있는 경우 loss값은 -log(1) 이므로 0이 된다. 반대로 정답 class를 하나도 못맞추게 되면 loss값은 -log(0) 이므로 ∞가 된다. 그러나 finite precision에서는 이러한 minumun value와 maximun value를 볼 수 없다.
Q2. Usually at initialization W is small so all s ≈ 0. What is the loss?
A. -log(1/C) = log(C)
SVM과 마찬가지로 sanity check를 진행할 수 있다.
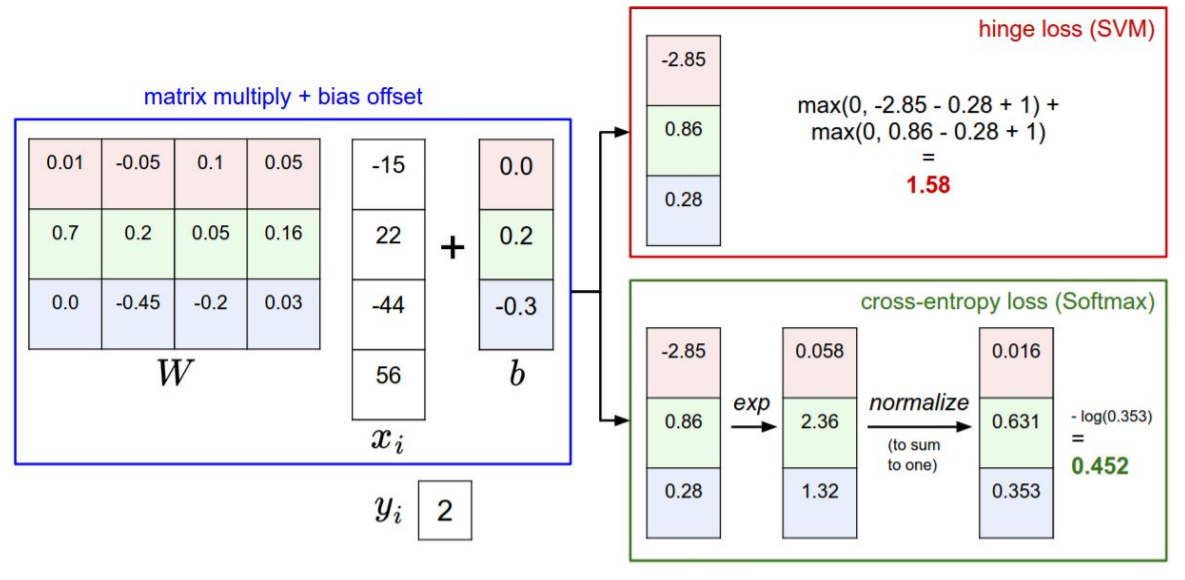
Q3. Suppose I take a datapoint and I jiggle a bit (changing its score slightly). What happens to the loss in both cases?
A. SVM의 경우는 정답의 score가 다른 score보다 얼마나 큰 값을 가지는지를 보았기 때문에 변화가 없었다. 그러나 softmax는 다르다. 정답 score가 높아지는 경우 softmax loss는 ∞로 가게 되고, 다른 label들의 loss는 -∞로 가게 된다.
How do we find the best W?
Optimizer
Strategy #1: A first very bad idea solution: Random search
W값을 랜덤하게 설정하여 진행

완전 무작위의 경우 10%이나 Random search의 경우 15%의 정확도를 보임(SOTA는 95%)
Strategy #2: Follow the slope
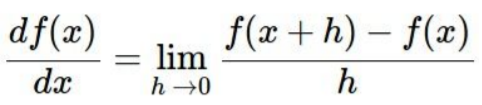
그래프의 미분값이 gradient가 된다. mulitple dimension의 경우 gradient는 각 dimension에 대한 편미분 값이다.
어느 방향으로의 slope는 dot product of the direction with the gradient 이다
가장 가파른 내리막 방향은 음의 기울기를 가진다(loss값이 작아지도록 함)

Loss 값을 구하는 함수로 계산하면 훨씬 빠르게 dW값을 구할 수 있다.
- Numerical gradient: approximate, slow, easy to write
- Analytic gradient: exact, fast, error-prone
Gradient Descent

Gradient Descent를 전체 데이터셋으로 진행할 때, 데이터셋의 양이 많아지면(imagenet = 1.3 B) 한번 업데이트 하는데 많은 시간을 소모하게 된다. 이를 해결하기 위해 나온 방법이 Stochastic gradient descent 이다
Stochastic gradient descent은 전체에 대해 loss과 gradient를 계산하는 대신, 32, 64, 128 등 sample을 추출해서 이 데이터들을 이용하여 loss와 gradient를 구하게 된다.

Aside : Image Features
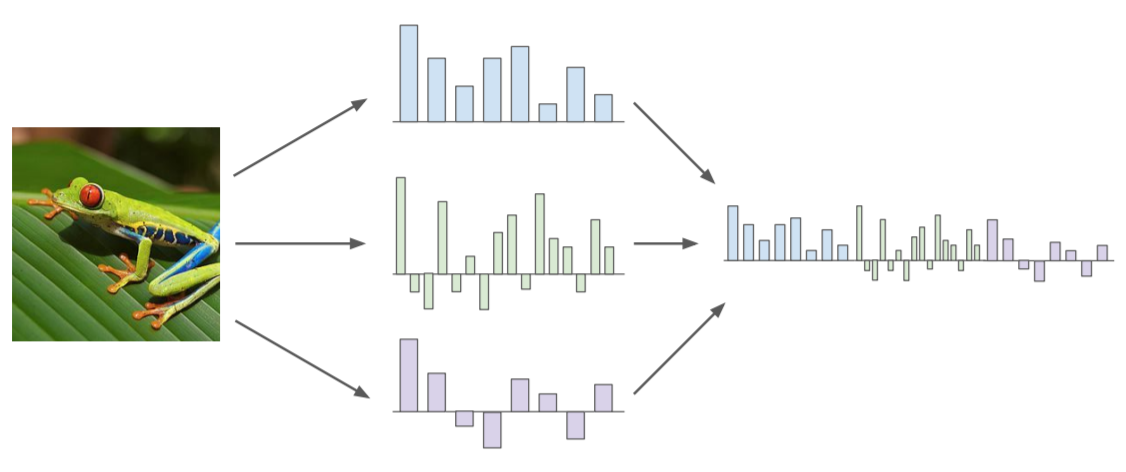
Image Features : Motivation
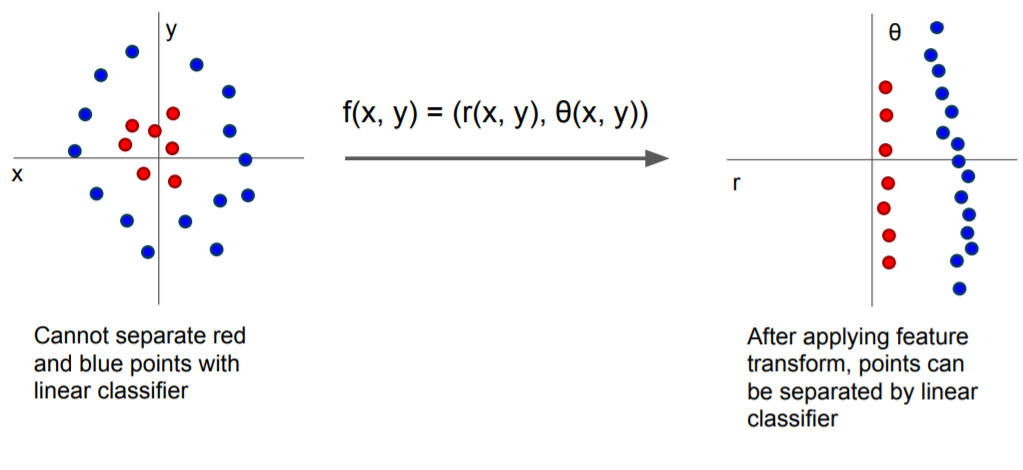
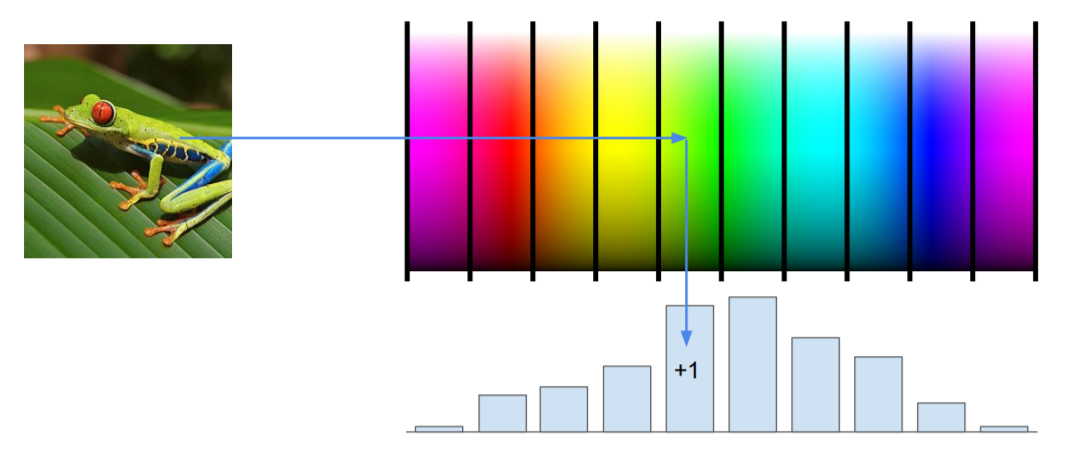
Example: Color Histogram
Example: Histogram of Oriented Gradients (HoG)

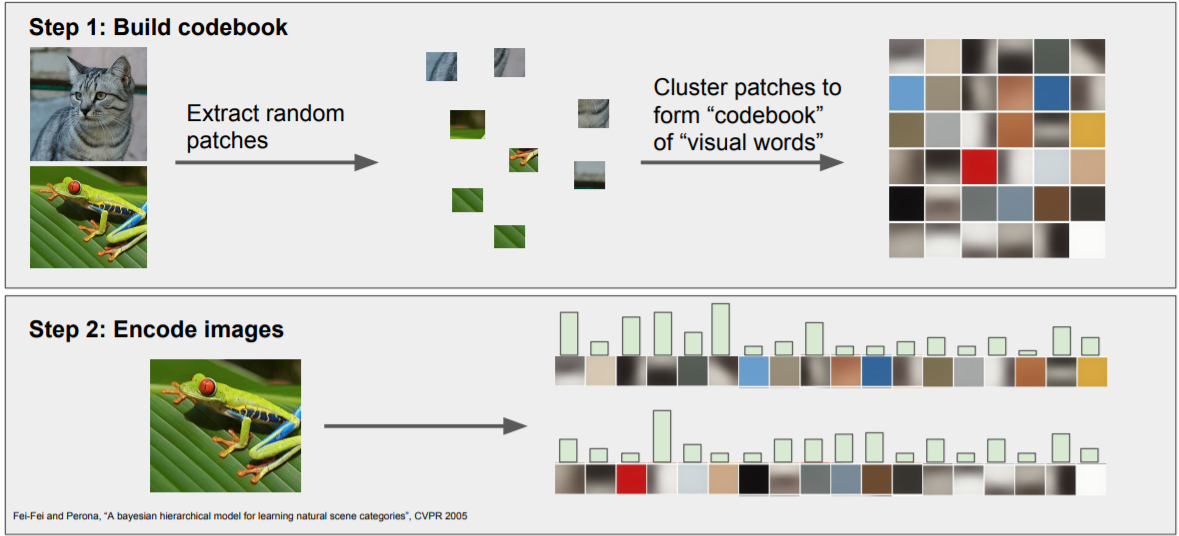
Example: Bag of Words
'Study > CS231n' 카테고리의 다른 글
| Lecture 7 . Training Neural Networks II (0) | 2022.02.14 |
|---|---|
| Lecture 6. Training Neural Networks I (0) | 2022.02.07 |
| Lecture 5. Convolutional Neural Networks (0) | 2022.01.21 |
| Lecture 4. Introduction to Neural Networks (0) | 2022.01.13 |
| Lecture2. Image Classification (0) | 2022.01.10 |




댓글