Lecture2. Image Classification

본 글은 Stanford University CS231n 강의를 듣고 정리한 내용입니다.

• K_Nearset Neighbor
• Linear classifiers : SVM, Softmax
• Tow-layer nerual network
• Image features

Image Classification

이러한 이미지를 정해진 discrete labels set 중에 하나의 class로 지정하게 된다.

사람에겐 쉽지만 computer 에겐 매우 어려운 일입니다.

왜냐하면 컴퓨터가 보는 이미지는 0과 255 사이의 숫자들로 이루어져 있기 때문이다.

이러한 픽셀값들은 객체가 움직이거나, 카메라의 앵글이 조금만 달라져도 모두 다른값으로 바뀐다. 

그러나 픽셀값들이 모두 바껴도 같은 고양이를 나타낸다.

알고리즘은 이러한 경우에 대해 robust 해야한다.

brightness가 다른 경우에 대해서도 마찬가지로 robust 해야함

다양한 pose에 대해서도 robust 해야함

일부분이 가려진 경우에 대해서도 robust 해야함

배경과 비슷한 색을 가지는 경우

사람의 뇌는 이러한 경우를 구분할 수 있지만, 컴퓨터에게 이러한 문제는 매우 도전적인 과제이다.

visual recognition를 위해 edge는 매우 중요하다는 것을 알고있다. 이를 위해 이미지에서 edge를 추출하고, corner와 boundaries들을 categorize하게 된다. 이를 통해 고양이를 구분하는 rule이 생성되게 된다.

그러나 이 방법은 단점이 있다.

1. Super brittle
2. 다른 카테고리의 경우 새로 시작해야 한다.

고양이는 무엇이다, 물고기는 무엇이다 식으로 직접 규칙을 정하는 것이 아닌 Data-Driven Approach 방식으로 접근한다

Data-Driven Approach

1. Collect a dataset of images and labels
2. Use Machine Learning to train a classifier
3. Evaluate the classifier on new images

1 function(make a rule) -> 2 function(train the model, predict the result)

Nearest Neighbor

test images and nearest neighbors

항상 같은 class의 사진을 가지고 오지는 않지만, 다른 class의 사진이더라도 비슷한 특징을 보인다.

test image와 neighbors image 간의 차이를 비교하는 방법은 여러가지가 있다. 이 슬라이드에서는 L1 distance(Manhattan distance)를 사용한다.

L1 distance = sum(test image - training image)

 

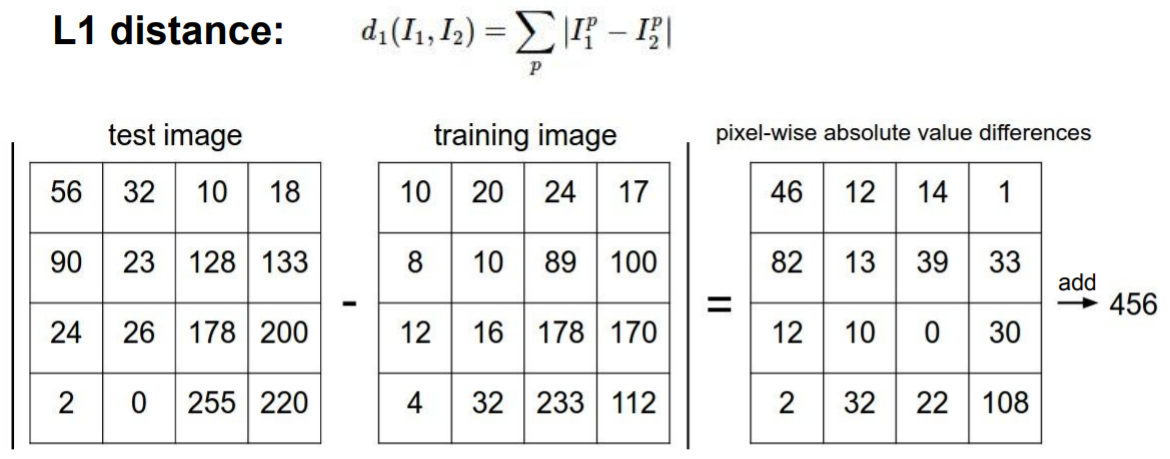
Q1. With N examples, how fast are training and prediction?

A : Train O(1), predict O(N)

what we want is fast at prediction, slow for training is OK

 

K-Nearest Neighbors

Instead of copying label from nearest neighbor, take majority vote from K closest points

 

bigger K, smooth out decision boundaries

k값을 키워주면 정확히 일치하지 않는 케이스도 많이 포함된다

 

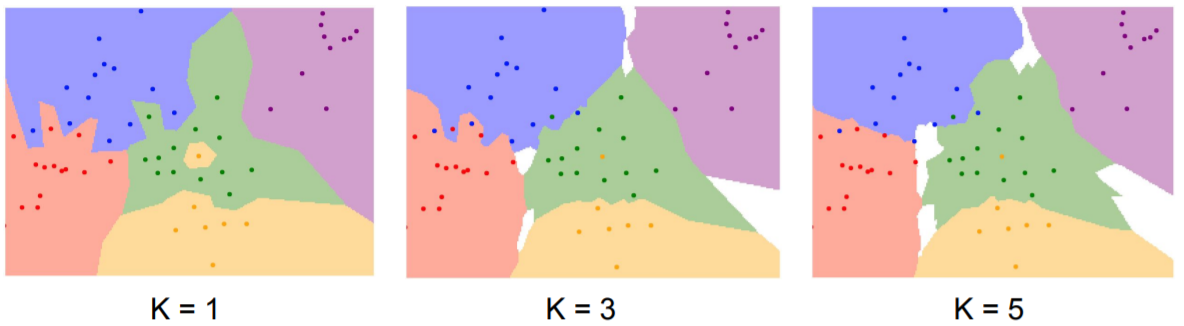
Distance Metric

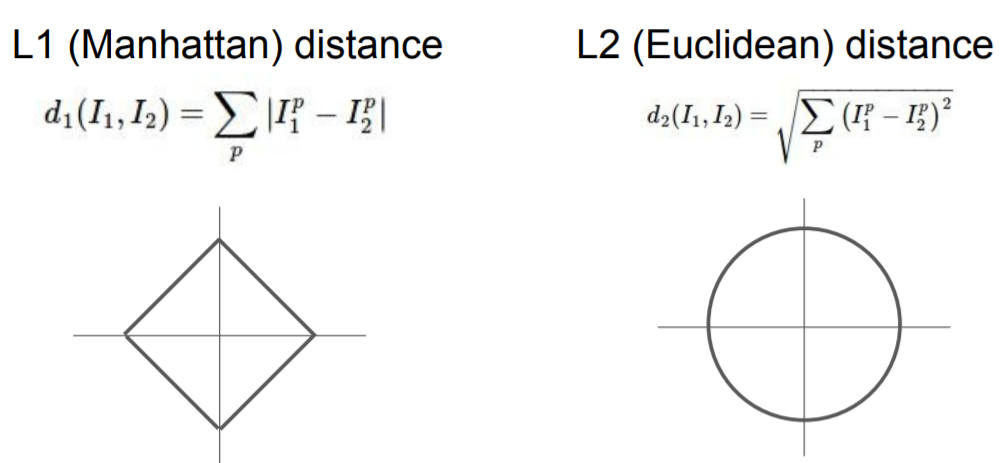
L1 distance는 이미지를 회전할 경우 L1 distance를 바꾸는 것이 된다.

image의 요소들이 개별적인 의미를 가지고 있다면 L1 distance가 더 잘 어울릴 수도 있는 반면, 그 외의 경우는 L2 distance가 더 잘 어울릴 수 있다.

여러가지 distance를 사용하여 generalize 할 수 있다.

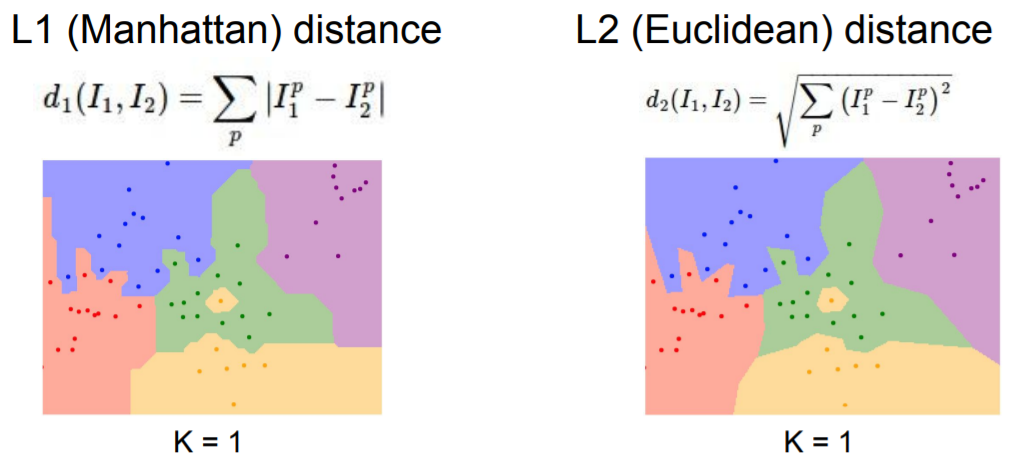
choice K, metrics -> hyperparameters

Setting Hyperparameters

1. Choose hyperparameters that work best on the data(BAD)
   1. K = 1 always works perfectly on trainin data
2. Split data into train and test, choose hypterparameters that work best on test data(BAD)
   1. No idea how algotirhm will perform on new data
3. Split data into train, val and test; choose hyperparameters on val and evaluate on test(Better!)
4. Cross-Validation : Split data info folds, try each fold as validation and average the results

 

value k에 대한 5-fold cross validation

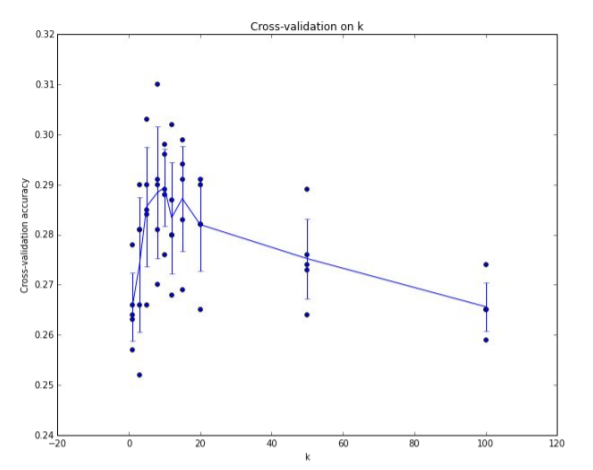
The line goes through the mean, bars indicated standard deviation

위 경우는 K가 7일 때 가장 좋은 결과를 나타내는 것으로 보인다.

 

그러나 KNN은 이미지에 절대 사용되지 않는다.

• test time이 매우 느리다.
• pixels의 Distance metrics 가 informative하지 않다.

all 3 images have same L2 distance to the one on the left

L2 distance를 사용하게 되면 full description of distance or difference between image를 잡아내지 못한다. 위 경우는 여러개의 original image를 가지는 것으로 간주된다.

 

• Curse of dimensionality

dimension이 늘어남에 따라 number of training sample의 갯수는 기하급수적으로 늘어나게 된다.

 

Linear Classification

 

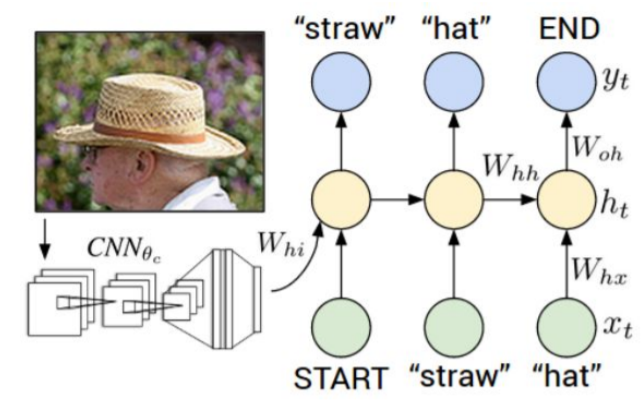
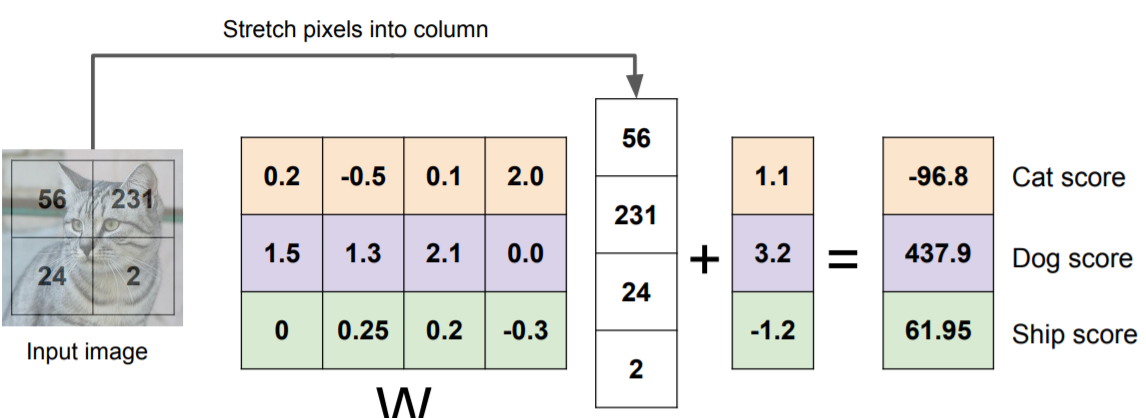
Parametric Approach

x : image data

W : parameters, weights

KNN 알고리즘과 다르게 학습 후 test 과정에서는 train 이미지는 필요하지 않고 parameter 값인 W만 필요하다.

Linear Classifier

CIFAR-10 데이터셋으로 학습된 linear classifier의 trained weights 예시는 다음과 같다.

plane class의 경우 linear classifier를 통과해서 나온 결과는 blue blob의 형태를 띈다.

Linear classifier의 단점은 각 클래스에 대해 1개의 template만 학습한다는 것이다.

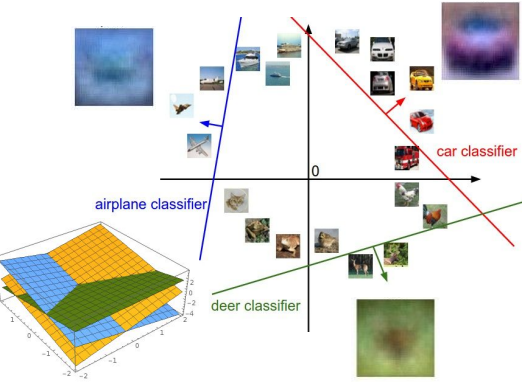
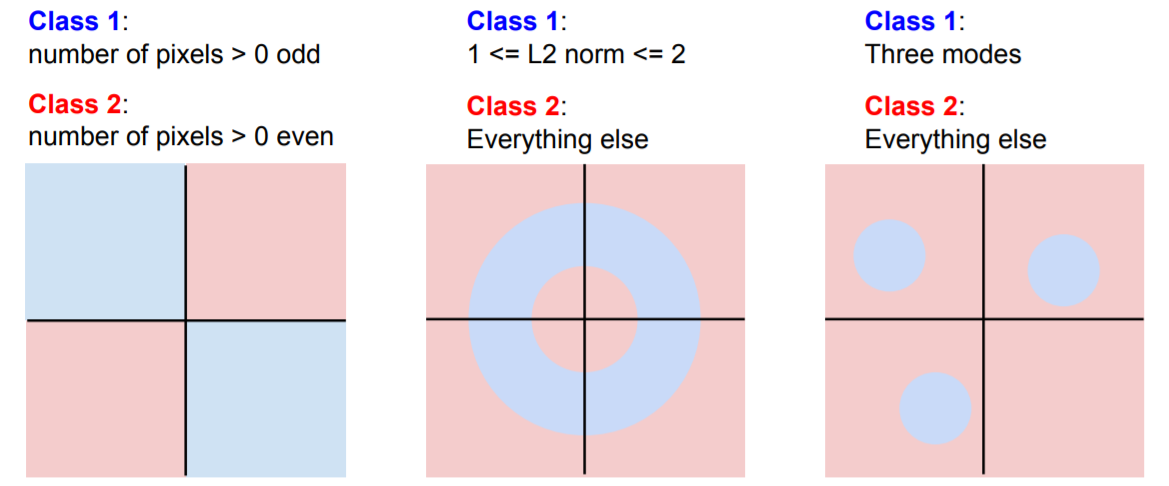
Hard cases for a linear classifier

 

 

출처: http://cs231n.stanford.edu/2017/index.html