Lecture 4. Introduction to Neural Networks

본 글은 Stanford University CS231n 강의를 듣고 정리한 내용입니다.

 

Computational graphs

forward propagation

1.  weight W와 data x가 만나 score를 출력한다.

2. hinge loss를 통해 L_i값을 구하고, regularization까지 더하여 최종 loss L을 출력한다.

 

Backpropagation

e.g. x = -2, y = 5, z = -4

f(x, y, z) = (x + y)z

Chain rule

result of backpropagation

∂f / ∂f = 1

∂f / ∂z = q = 3

∂f / ∂q = z = -4

∂f / ∂x = ∂f / ∂q * ∂q / ∂x = z * 1 = - 4

∂f / ∂y = ∂f / ∂q * ∂q / ∂y = z * 1 = -4

한 node에 대한 backpropagation을 위한 편미분

Chain rule = upstream gradient * local gradient

 

example of backpropagation

sigmoid function in ex node

정방향으로 진행하게 되면 sigmoid 함수가 되고, backpropagation으로 진행하면 sigmoid 함수를 미분한 값에 대한 함수가 된다.

 

Patterns in backward flow

add gate : gradient distributor(upstream의 gradient를 똑같이 여러 개에 전달해준다)

 

Q : What is max gate?

A : return maximun value.

Local gradient of max gate is z for z and 0 for w(add gate value for max value, 0 for non-max value)

 

max gate : gradient router(Max의 인자가 여러개라면 Max pooling이라고 보면 된다.)

 

Q : What is a mul gate?

A : Gradient를 서로 바꿔준다.

 

mul gate : gradient switcher(두 노드의 곱을 미분하면 상대 노드의 값이 남게 되기 때문)

 

x, y, z 값이 vector라면 달라지는 점은 local gradient가 Jacobian matrix가 된다는 것 뿐이다.

 

Vectorized operations

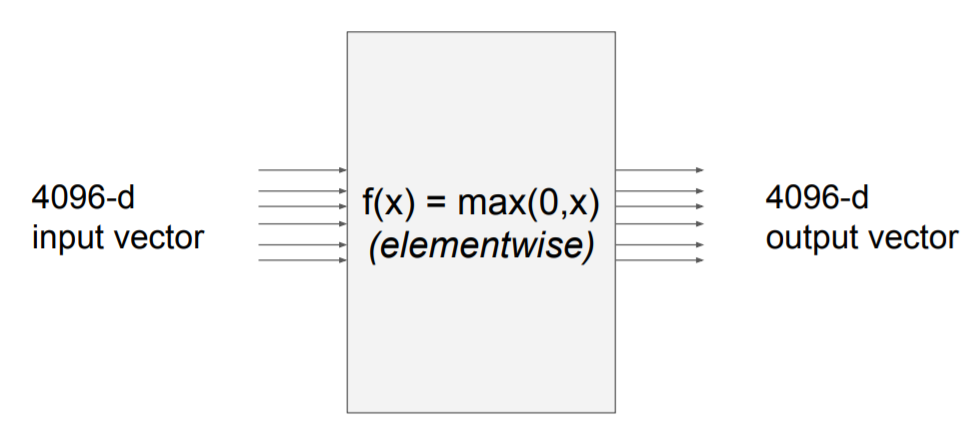
Q1 : What is the size of the jacobian matrix?

A : 4096 x 4096

위 상황에서 minibatch(100)을 사용하게 된다면 jacobian matrix의 크기는 409600 x 409600 이 된다

 

Q2: what does it look like?

A : Diagonal (첫번재 input은 첫번째 output에만 영향을 미쳐야 하기 때문에 대각행렬이다.)

 

x is n-dimensional, W is nxn-dimensional

q와 f equation

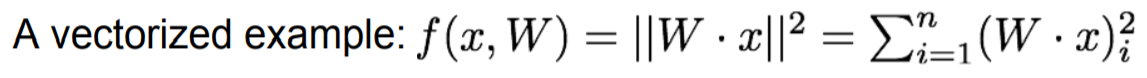
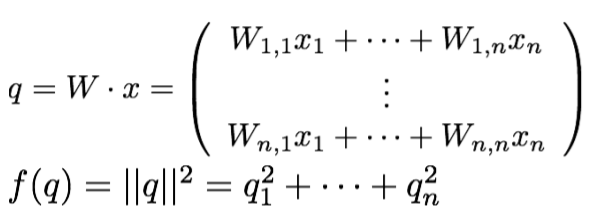
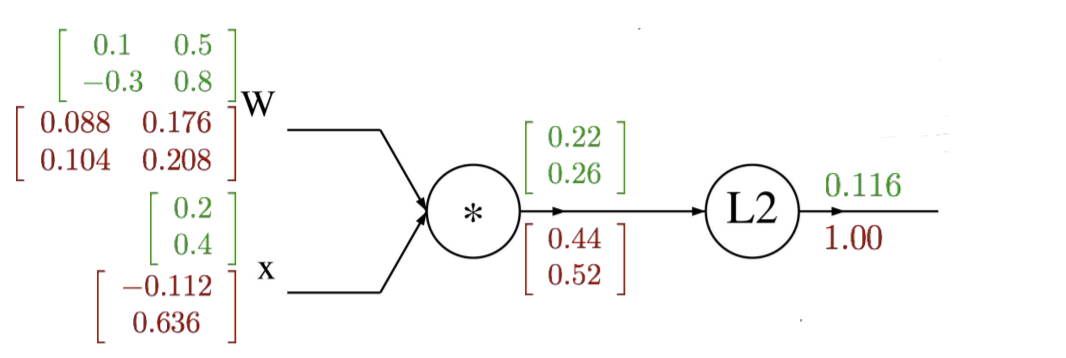
∂f / ∂f = 1

∂f / ∂q_i = 2q_i

∂q_k / ∂W_i,j = 1_(i=k) *x_j -> (q_1 = W_1,1*x_1 + W_1,2*x_2) -> i과 k값이 다른 경우는 편미분값이 존재할 수 없음

∴ ∂f / ∂W_i,j = 2q_i * x_j

∂q_k / ∂x_j = W_k, j

∴ ∂f / ∂x_j = 2q_i * W_i,j

 

Psuedo code of Graph Object

 

 

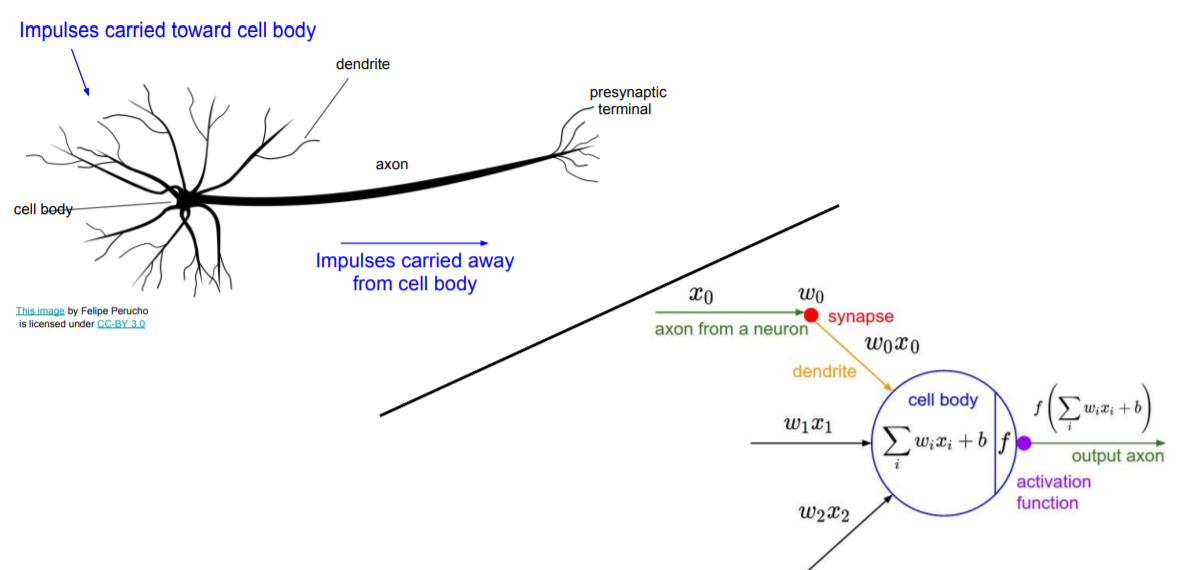
Neural Networks

Linear function : f = Wx -> 2-layer Neural Network f = W_2max(0, W_1x)

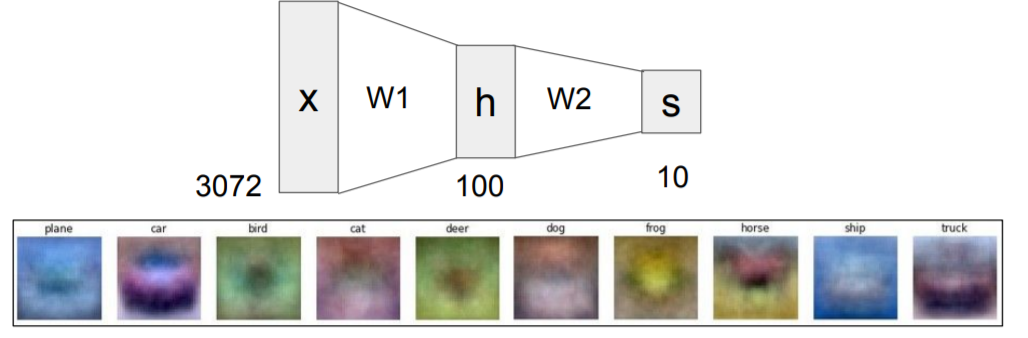
기존 linear function에서는 1개의 template만을 가질 수 있었으나, 2-layer에서는 이러한 단점을 보완할 수 있다.

W1에서는 기존보다 많은 template를 담을 수 있고, W2에서는 모든 templates들의 weighted sum을 구하게 한다. 이를 통해 다양한 templete의 점수들을 반영해서 class score를 더 잘 예측할 수 있게 됩니다.

 

ex. image가 left face horse일 때, h 에는 left-face horse에 대한 high score와 right-face horse에 대한 lower score가 있을것이다. W2는 이러한 값들의 weighted sum(w1x1 + w2x2 + ...)를 구하게 한다. 이를 통해 medium값을 나타내게 되고, any kind of horse에 대해 generally high score를 받게 된다.

 

 

neuron에서 신호의 이동, 실제 뇌와 신경망구조는 다르기때문에 직접적인 비교는 조심해야한다.

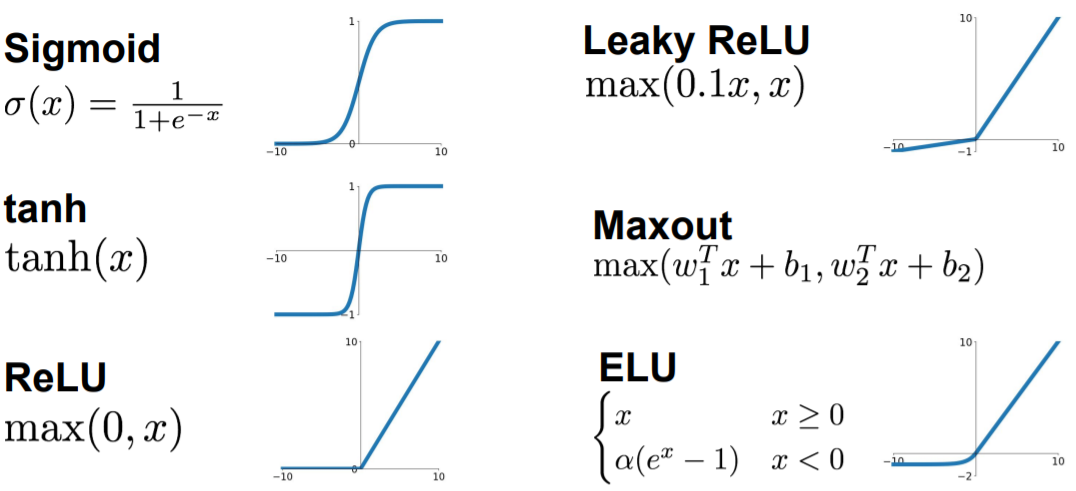
Activation Function

 

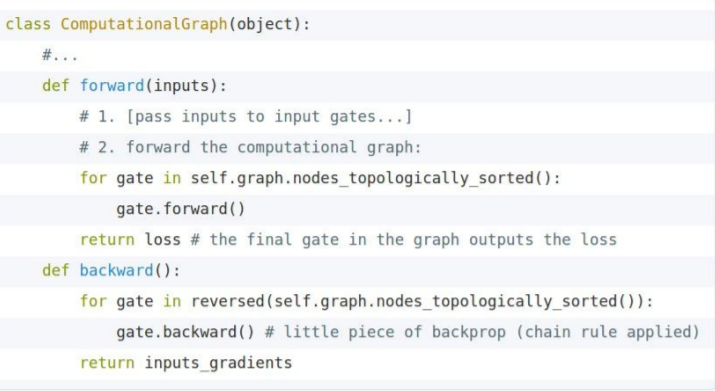
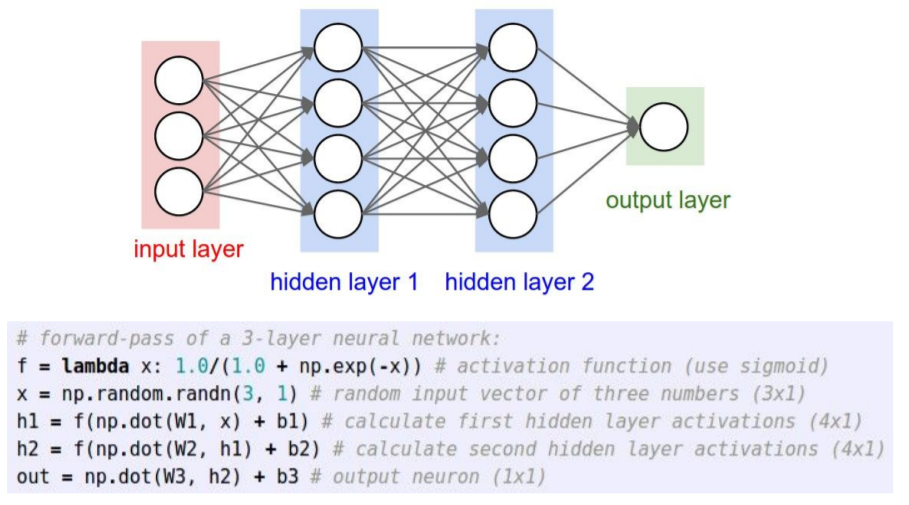
Example feed-forward computation of a neural network

input vector x 가 layer들을 통과하는 과정을 나타낸 code

 

 

출처: http://cs231n.stanford.edu/2017/index.html

https://yunmap.tistory.com/entry/Deep-Learning-cs231n-4%EA%B0%95-%EB%82%B4%EC%9A%A9-%EC%A0%95%EB%A6%AC-1