Lecture 5. Convolutional Neural Networks

본 글은 Stanford University CS231n 강의를 듣고 정리한 내용입니다.

 

Convolutional Neural Networks

A bit of history...

 

Fully Connected Layer

32x32x3 image -> stretch to 3072 x 1

3072 dimension을 가진 10개의 행에 대한 dot product를 진행한다.

Convolution Layer

filter의 depth는 언제나 image의 depth와 같아야 한다.

• 필터와 5x5x3 chunk of image 사이의 dot product 값이 1개가 나오게 된다. 하나의 결과를 뽑아내기 위해 5*5*3 총 75-dimensional dot product + bias 를 진행하게 된다.
• 위 연산은 5x5x3의 chunk를 linear하게 편 후 계산하는 것과 동일하다.
• 전체 spatial locations을 slide한 결과로 28x28x1의 activation map을 출력한다.

filter의 갯수를 지정해 주는 만큼 activation map이 출력되게 된다. 위 예시에서는 6개의 5x5 filter를 지정해주었기 때문에, 28x28x1의 activation map이 총 6개가 출력된다.

 

ConvNet 예시

input과 가까이 있는 Convolutional layer는 low-level의 feature(ex. edges)를 추출하게 되고, middle level의 layer는 보다 복잡한 feature(ex. corners, blobs)를 추출하게 된다. high level feature는 blob보다는 concept를 닮아가게 된다.

 

Ex. 7x7 input assume 3x3 filter

5x5 output

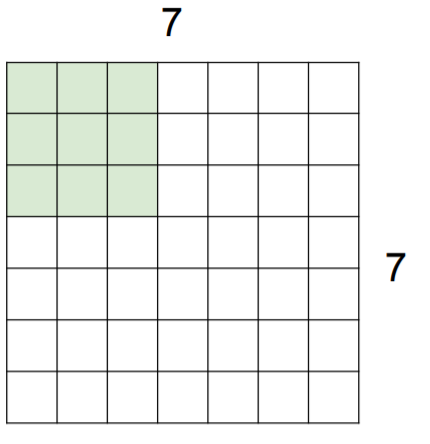
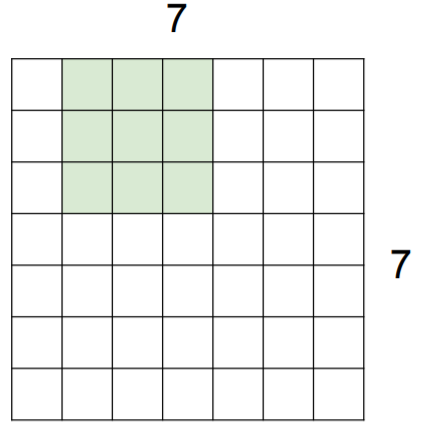
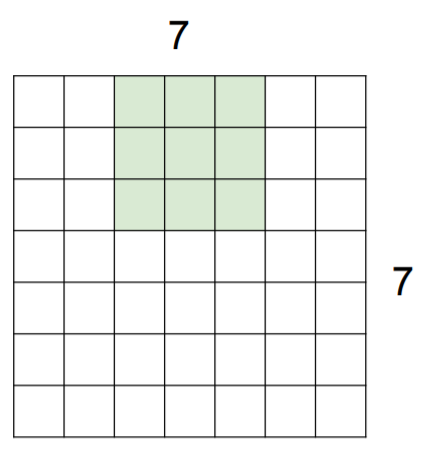
Ex. 7x7 input assume 3x3 filter with stride 2

3x3 output

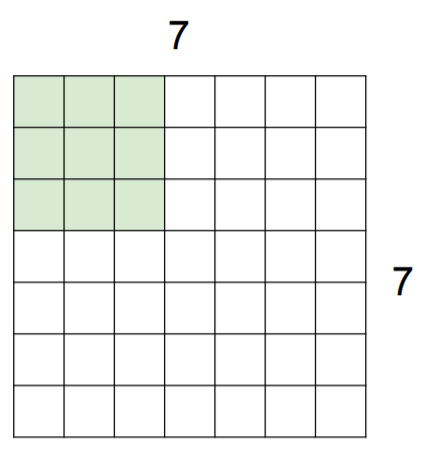
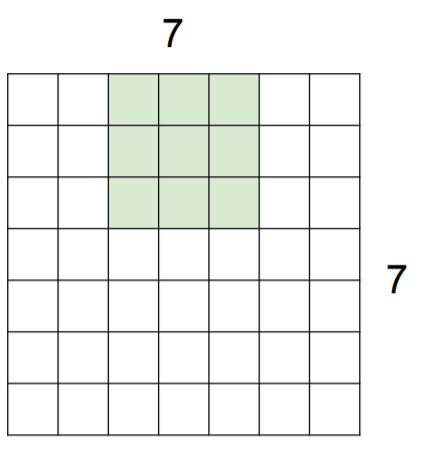
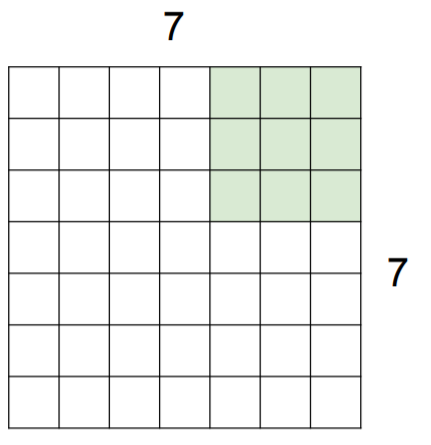
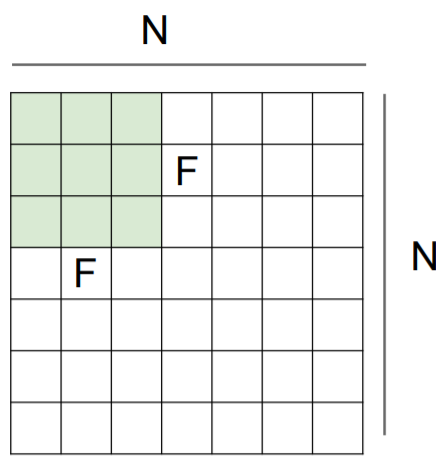
Ex. 7x7 input assume 3x3 filter with stride 3

-> doesn’t fit! cannot apply 3x3 filter on 7x7 input with stride 3.

 

∴ Output size: (N - F) / stride + 1

Ex. input 7x7, 3x3 filter, applied with stride 1 pad with 1 pixel border

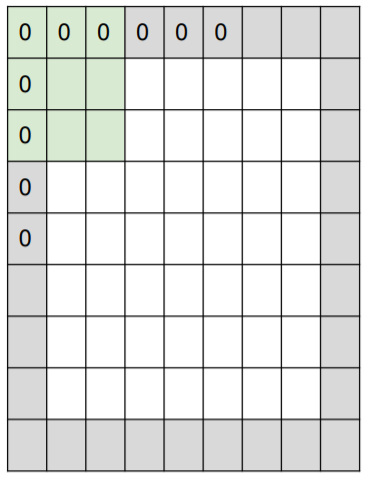
output size = (9 - 3) / 1 + 1 = 7 -> 7x7 output!

 

Q. A -> Edge에 대한 검출을 하기 위해 zero padding을 해야 하는건 아니지만 합리적인 방법이기 때문에 사용한다.

Q. A -> Zero padding을 하는 이유는 output size를 input size와 동일하게 만들어 주기 위함이다.

 

Example

Input volume: 32x32x3, 10 5x5 filters with stride 1, pad 2 -> output size?

output size = (32+2 * 2 - 5) / 1 + 1 = 32

∴ 32x32x10

 

Number of parameters in this layer?

each filter has 5*5*3 + 1 = 76 params (+1 for bias) => 76*10 = 760

 

Summary

Filter의 크기는 1, 3, 5와 같은 방식으로 주로 결정

Stride는 주로 1이나 2를 사용

Padding은 알맞은 값 사용

Number of filters는 주로 2의 제곱수를 사용한다.(e.g. 32, 64, 128, 512)

 

The brain/neuron view of CONV Layer

filter의 크기만큼 image에서 연산을 진행하기 때문에 receptive field와 크기가 같다

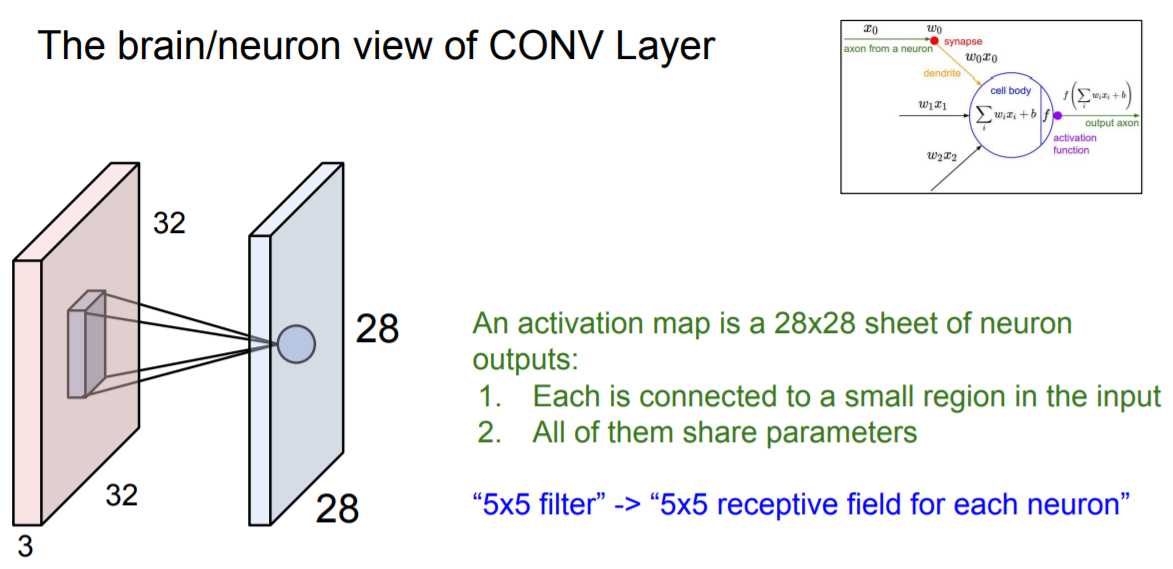
5x5 receptive field와 5x5 filter간의 연산으로 하나의 값이 나오게 되는데 이는 앞서 봤던 dot product와 같은 아이디어로 진행된다.

input이 들어오면 이 값이 synapse w(weight)를 거쳐 하나의 값을 출력하게 된다.

여기서 다른 점은 convolution 연산의 경우 전체가 아닌 5x5의 local region에 대한 연산만을 하게 된다.

 

Pooling layer

makes the representations smaller and more manageable

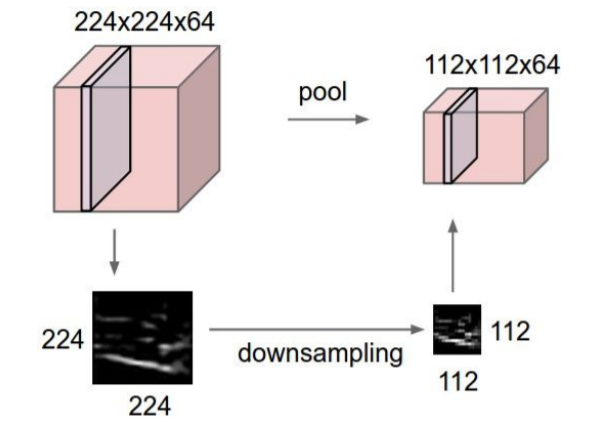
Pooling layer가 하는 일은 downsampling을 하는 것이다.

즉, Pooling layer는 Representation들을 더 작고 관리하기 쉽게 만들어 주는 것이다.

pooling layer는 depth값은 건들지 않기 때문에 depth값은 변하지 않는다.

Max Pooling

Conv layer를 지난 후의 값들은 how much this filter fired in this location을 나타내게 된다.

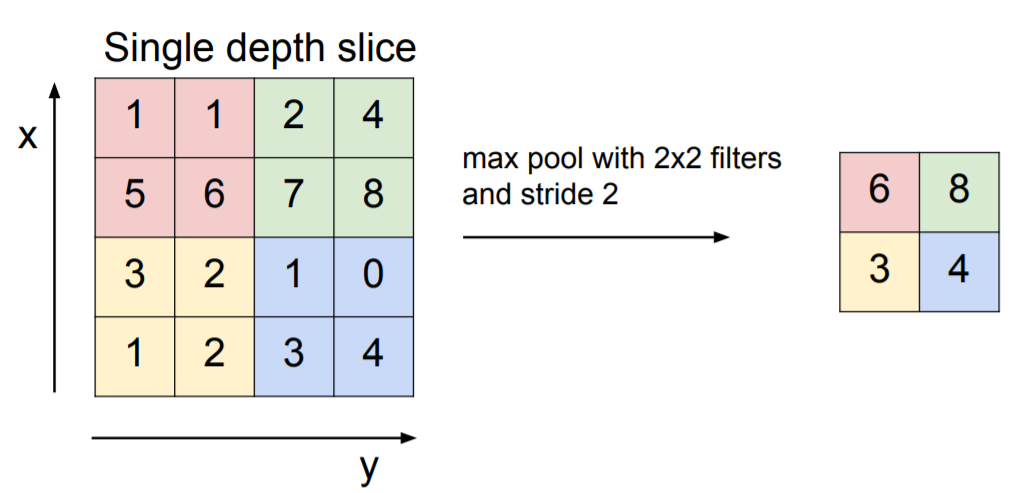
pooling을 하는 경우는 filter가 같은 영역을 여러번 보지 않도록 stride값을 조절해준다.

 

Filter의 크기는 2, 3을 주로 사용

Stride는 주로 2를 사용

 

위 사진에서는 Conv layer와 앞 시간에 배운 ReLU레이어를 통과시킨 후 Pooling을 진행해준다. Network의 마지막에는 Fully-Connected layer가 위치하게 된다. Fully-Connected layer는 a x b x c의 형태인 마지막 Pooling output을 1-dimension으로 바꿔주는 역할을 하게 된다.

 

 

 

출처: http://cs231n.stanford.edu/2017/index.html